What Is The Potential Energy Of A System Of Particles?
Potential energy is the stored energy an object or system of objects has due to their position or arrangement. For a system of particles, the potential energy is the sum of the potential energies for each individual particle based on the forces acting on it within the system. Calculating the potential energy allows us to determine how much work can be done on or by the system as the particles interact and change positions. Understanding potential energy is key for analyzing many mechanical, electrical, chemical, and even biological systems.
This article will provide an overview of potential energy in the context of systems of particles. We will explore the different types of potential energy, how to calculate it, and how potential energy diagrams can model interactions and changes in systems. Real-world applications will also be discussed.
Calculating Potential Energy
The potential energy of a system depends on the configuration of that system and the forces acting on it. To calculate potential energy, we apply formulas that incorporate information about the system such as mass, height, distance between objects, spring constants, charges, etc. The most common potential energy formulas include:
Gravitational potential energy: PEgrav = mgh, where m is mass, g is gravitational acceleration, and h is height.
Elastic potential energy: PEelastic = 1/2kx2, where k is the spring constant and x is the displacement from the spring’s rest position.
Electric potential energy: PEelectric = kq/r, where k is Coulomb’s constant, q is electric charge, and r is distance between charges.
To calculate potential energy, we plug the values relevant to our system into the appropriate equation. For example, to find the gravitational potential energy of a 5kg object lifted 2m above the ground on Earth, we calculate PEgrav = mgh = (5kg)(9.8m/s2)(2m) = 98 J. The more we know about the properties of the system, the more precisely we can determine its potential energy.
Gravitational Potential Energy
The gravitational potential energy of a system of particles is equal to the negative of the work done by the gravitational force in assembling the system. The formula for gravitational potential energy is:
GPE = -GMm/r
Where G is the universal gravitational constant, M is the mass of one particle, m is the mass of the other particle, and r is the distance between the two particles.
For example, let’s calculate the gravitational potential energy of a simple two particle system – the Earth and the Moon. The mass of the Earth is 5.97 × 1024 kg. The mass of the Moon is 7.34 × 1022 kg. The distance between them is 384,400 km on average. Plugging this into the formula:
GPE = -GMm/r
GPE = -(6.67 × 10-11 Nm2/kg2) * (5.97 × 1024 kg) * (7.34 × 1022 kg) / (384,400,000 m)
GPE = -1.99 × 1028 J
So the gravitational potential energy of the Earth-Moon system is -1.99 × 1028 J. This shows that a tremendous amount of work would need to be done to separate the two bodies from each other against the force of gravity.
We can calculate the GPE for any system of multiple particles using the same approach. Just sum up the individual GPE for each pair of interacting particles based on their masses and separation distance.
Elastic Potential Energy
Elastic potential energy is the energy stored in elastic materials that are deformed. It arises due to the stretching or compressing of bonds between atoms in the material. The magnitude of the elastic potential energy is dependent on the stiffness of the material and the amount of deformation.
The formula for elastic potential energy is:
PEel = 1⁄2 kx2
Where:
- PEel is the elastic potential energy
- k is the spring constant of the material
- x is the displacement from the equilibrium position
As an example, consider a spring with a spring constant of 50 N/m. If the spring is stretched 0.2 m from its relaxed length, the elastic potential energy stored in the spring can be calculated as:
PEel = 1⁄2 (50 N/m) (0.2 m)2
= 2 Joules
The more a spring is stretched or compressed, the greater the elastic potential energy stored. This energy can be recovered when the spring returns to its original shape.
Electrical Potential Energy
Electrical potential energy exists between two charged particles or objects thanks to the electromagnetic force between them. It depends on the amount of charge on each object, q1 and q2, and the distance r between them. The formula for electrical potential energy is:
PE = kq1q2/r
Where k is a proportionality constant known as Coulomb’s constant. Some examples of calculating electrical potential energy:
– Between two point charges q1 = 2 μC and q2 = -6 μC separated by a distance r = 5 m, the potential energy is:
PE = (8.99 x 109 Nm2/C2) x (2 x 10-6 C) x (-6 x 10-6 C) / (5 m) = -215.76 J
– For two charged parallel plates with charge +Q and -Q, area A, and separated by distance d, the potential energy stored is:
PE = (Q2)/(2ε0A) x (1/d)
– In a capacitor with capacitance C storing charge Q, the electrical potential energy is:
PE = (Q2)/(2C)
In all cases, the potential energy increases as the charges get closer together, and decreases as they move apart.
Chemical Potential Energy
Chemical potential energy is the stored energy released when a chemical reaction or change in atomic configuration occurs. The formula for calculating chemical potential energy is:
PEchemical = ∆Hreaction
Where:
- PEchemical is the chemical potential energy (in Joules)
- ∆Hreaction is the enthalpy change of the reaction (in Joules)
Enthalpy change (∆H) is the heat released or absorbed during a chemical reaction at constant pressure. Exothermic reactions release energy (negative ∆H), while endothermic reactions absorb energy (positive ∆H).
For example, the enthalpy change for the combustion reaction of methane is:
CH4(g) + 2O2(g) → CO2(g) + 2H2O(l) ∆H = -890 kJ
So the chemical potential energy released is 890 kJ.
Another example is the enthalpy change for the reaction between baking soda (NaHCO3) and vinegar (CH3COOH):
NaHCO3(aq) + CH3COOH(aq) → CO2(g) + H2O(l) + Na+(aq) + CH3COO–(aq)
∆H = -27 kJ
Therefore, 27 kJ of chemical potential energy is released in this reaction when baking soda and vinegar are mixed.
Conservative vs Nonconservative Forces
When calculating potential energy, it’s important to consider whether the forces acting on the system are conservative or nonconservative. Conservative forces are forces that conserve mechanical energy. This means that when a conservative force acts, the work done by the force on the system equals the change in the system’s mechanical energy.
Some examples of conservative forces include gravitational force, spring force, and electrostatic force. The mechanical energy of a system with only conservative forces acting on it remains constant. This makes calculating potential energy more straightforward, since the work done to move between two positions in a conservative field depends only on the starting and ending positions.
On the other hand, nonconservative forces do not conserve mechanical energy. Friction is a common example of a nonconservative force. When nonconservative forces act on a system, the work done by the force does not equal the change in mechanical energy. This means the work done against nonconservative forces must be taken into account separately when calculating potential energy.
To summarize, conservative forces simplify potential energy calculations, while nonconservative forces require additional considerations to account for energy losses due to work done against them. Understanding the difference is key for accurately determining potential energy in real-world systems.
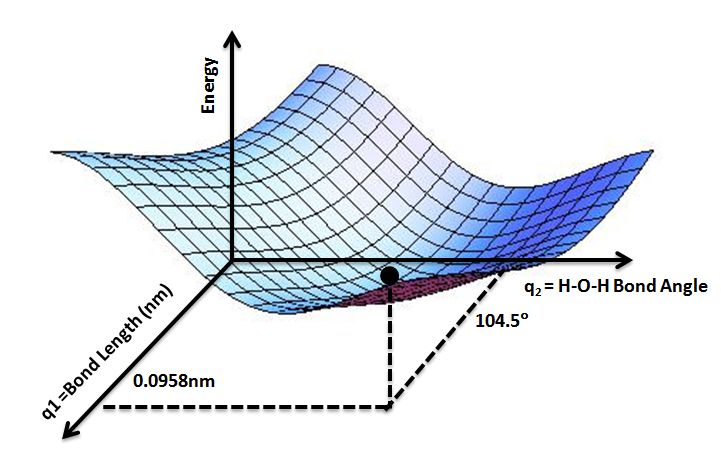
Potential Energy Diagrams
Potential energy diagrams, also known as potential energy curves, are graphical representations of the potential energy of a system as a function of position or configuration.
To construct a potential energy diagram:
- Identify the system and parameters that define its configuration (e.g. the positions of particles, bond lengths, angles between bonds, etc.)
- Calculate the potential energy of the system for different configurations.
- Plot the potential energy values on the y-axis versus the configuration parameter on the x-axis.
Key features of potential energy diagrams:
- The minimum points represent stable equilibrium configurations.
- Maximum points represent unstable equilibrium configurations.
- The slope indicates the restoring force acting on the system.
Potential energy diagrams help visualize how the potential energy changes during processes like chemical reactions, phase transitions, and molecular conformational changes. They provide insight into the stability, equilibrium configurations, and dynamics of systems.
Applications
Potential energy concepts have many important real-world applications in physics and engineering:
Renewable Energy: The potential energy stored in water held behind dams is harnessed to generate hydroelectric power. Pumped storage systems use gravitational potential energy to store energy and produce electricity during peak demand periods.
Batteries: Batteries utilize chemical potential energy through redox reactions to store and deliver electrical energy. The voltage of a battery directly relates to the chemical potential difference between the electrodes.
Capacitors: Capacitors store energy in the electric field between their plates. Increasing the voltage increases the electric potential energy that can be stored for later use.
Springs and Elastic Devices: The elastic potential energy stored in compressed or stretched springs, rubber bands, and other elastic materials can be used to absorb shock, exert forces, and do mechanical work.
Power Generation: The gravitational potential energy of falling water is used in hydroelectric dams to spin turbines. The kinetic energy of wind and tides is also converted into electricity using similar principles.
Roller Coasters: The changing gravitational potential energy of roller coaster cars as they go up and down hills is precisely calculated by engineers during design to maximize thrills while maintaining safety.
Conclusion
In summary, potential energy is the stored energy an object or system of objects has due to their position or arrangement. There are several main types of potential energy that are relevant for systems of particles, including gravitational potential energy due to height, elastic potential energy due to deformation, electrical potential energy due to charge separation, and chemical potential energy stored in molecular bonds. Both conservative and nonconservative forces can contribute to the potential energy of a system. Potential energy diagrams provide a useful visualization of how potential energy changes as particles in a system move to different positions.
Understanding potential energy is crucial for analyzing systems of particles across many scientific fields. Potential energy allows us to quantify the stored energy available to do work on particles as they interact and move around. Tracking changes in potential energy provides insights into the dynamics and stability of systems. Potential energy concepts inform everything from molecular binding to planetary orbits to bungee jumping. Whether designing new materials, building skyscrapers, or playing with gyroscopes and springs, the potential energy perspective provides a powerful toolkit for modeling our world.