What Is The Relationship Of Mass And Potential Energy?

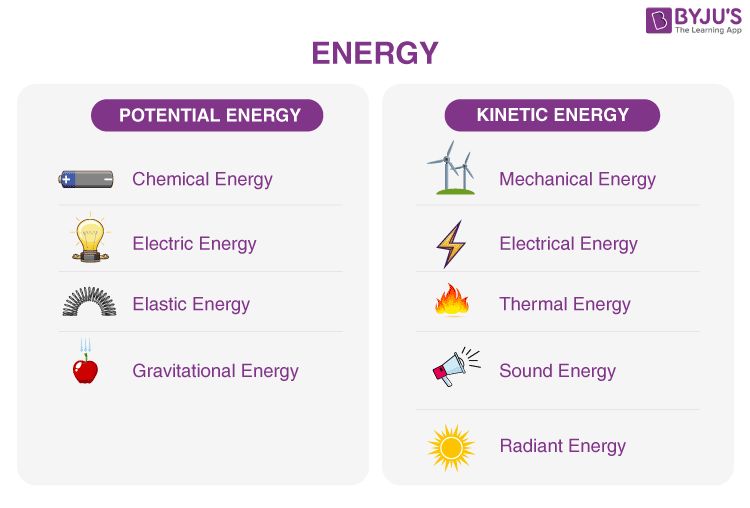
Mass is a property of matter that measures the quantity of matter in an object. It represents the amount of inertia or resistance to change in velocity that an object possesses. The standard unit of mass is the kilogram (kg). Potential energy is the stored energy an object has because of its position or configuration. There are different types of potential energy depending on the system, but they all refer to energy that has the potential to do work.

Mass and potential energy have a direct relationship with each other. In many systems, as the mass of an object increases, so does its potential energy. This is because potential energy depends on mass – the more massive an object is, the greater its potential energy could be. Understanding the link between mass and potential energy helps explain many physical phenomena and has important applications across science and engineering.

Mass

Mass is a measure of the amount of matter in an object. It is a fundamental property of an object that is independent of the object’s volume or shape. Mass is generally measured in kilograms (kg) in the International System of Units (SI).

The mass of an object can be measured using a balance scale. The object is placed on one side of the scale, while standard masses are incrementally added to the other side, until the scale balances. This allows the mass of the object to be determined relative to the known standard masses. Mass can also be measured in a laboratory using a mass spectrometer.

Some examples of objects with different masses:

• A feather has a very small mass, on the order of grams.
• A brick may have a mass of a few kilograms.
• A car has a mass of over 1000 kg.
• The Earth has a mass of around 6 x 1024 kg.

Potential Energy

Potential energy is the stored energy an object has due to its position or composition. There are several types of potential energy:

Gravitational Potential Energy

Gravitational potential energy is energy that depends on an object’s height above the ground. The higher the object is above the ground, the greater its gravitational potential energy. When the object falls, this potential energy gets converted into kinetic energy.

Elastic Potential Energy

Elastic potential energy refers to energy stored in elastic objects that are deformed. For example, stretching or compressing a spring stores elastic potential energy. When released, the spring converts the stored energy into kinetic energy.

Chemical Potential Energy

Chemical potential energy is energy stored in the bonds between atoms and molecules. This energy can be released in chemical reactions when the molecules rearrange into more stable configurations.

Nuclear Potential Energy

Nuclear potential energy arises from the strong nuclear forces between protons and neutrons in an atomic nucleus. Nuclear potential energy can be released by nuclear fission or fusion.

Direct Relationship

There is a direct relationship between mass and potential energy. As mass increases, potential energy also increases. This is because potential energy is directly proportional to mass according to the equation:

PE = mgh

Where PE is potential energy, m is mass, g is the gravitational acceleration constant, and h is height. The mass term in the equation demonstrates that as mass increases, so does potential energy. This makes intuitive sense – the more massive an object, the more energy is required to move it to a higher position.

For example, lifting a 10 kg weight to a height of 2 meters requires more energy than lifting a 5 kg weight to the same height. The 10 kg weight has more potential energy at the 2 meter height. This illustrates the direct relationship between mass and potential energy.

Gravitational Potential Energy

Gravitational potential energy is the energy an object possesses because of its position in a gravitational field. The gravitational potential energy equation demonstrates the direct relationship between an object’s mass and its potential energy:

Gravitational Potential Energy = mgh

Where m is the mass of the object, g is the gravitational acceleration constant, and h is the height of the object. The key thing to notice in this equation is that as the object’s mass increases, the gravitational potential energy increases proportionally. In other words, an object with twice the mass at a given height would have twice the gravitational potential energy. This shows how mass and gravitational potential energy have a direct relationship – the greater the mass, the greater the gravitational potential energy.

This direct relationship exists because the mass of an object determines the strength of its gravitational attraction to other masses. More massive objects experience a stronger gravitational force. When held at a height, more massive objects have the potential to release more energy upon falling towards the Earth, hence they possess more gravitational potential energy. The mass term in the gravitational potential energy equation accounts for this direct proportionality.

Elastic Potential Energy

Elastic potential energy is the energy stored in elastic materials that are stretched or compressed. A classic example is a stretched rubber band. When the rubber band is stretched, energy is required to deform the chemical bonds in the material. This energy is stored in the deformed bonds. The more the rubber band is stretched, the more elastic potential energy it has.

The elastic potential energy of a stretched object can be calculated using the equation:

Elastic Potential Energy = (1/2)kx2

Where k is the spring constant of the material, and x is the displacement or deformation from the rest position. The spring constant depends on the elastic properties of the material.

The key thing to notice in this equation is that the elastic potential energy scales with the square of the displacement x. So if you double the displacement, the elastic potential energy will increase by a factor of 4. This shows the direct proportional relationship with mass. If an object with twice the mass stretches the spring by a factor of 2, the resulting elastic potential energy will be 4 times greater.

Materials like springs, rubber bands, trampolines, slingshots, and bungee cords all exhibit elastic potential energy when deformed. This energy can then be harnessed to do work. For example, the tension force in a stretched rubber band can accelerate a projectile. The elastic properties of materials make elastic potential energy useful in many engineering applications.

Examples

Here are some real-world examples that demonstrate the direct relationship between mass and potential energy:

Gravitational Potential Energy

When you lift an object upwards, you are moving it against the pull of gravity. The higher it goes, the more gravitational potential energy it has. Doubling the mass of the object (while keeping the height the same) doubles the gravitational potential energy.

Bungee Jumping

The gravitational potential energy of a bungee jumper depends on their mass and height above the ground. A heavier jumper at the same height will have more gravitational potential energy.

Roller Coaster

Roller coasters utilize the conversion between gravitational potential energy at the top of a hill and kinetic energy as the coaster speeds downhill. The more massive the roller coaster car and passengers, the more potential energy stored when lifted up the hill.

Spring

Stretching or compressing a spring stores elastic potential energy. The same spring compressed to the same position will store twice as much elastic potential energy if the mass at the end is doubled.

Trampoline

A heavier person on a trampoline will rebound higher than a lighter person, as more elastic potential energy is stored in the trampoline springs during the jump.

Applications

The relationship between mass and potential energy has many important applications in the real world.

In physics, this relationship allows us to calculate the potential energy of objects based on their mass and height, which is critical for analyzing mechanical systems and motions. For example, knowing the gravitational potential energy of a ball based on its mass and height above the ground helps predict and explain its motion when dropped.

In engineering, understanding potential energy is key for designing many systems and devices. Mechanical engineers may leverage gravitational potential energy by lifting heavy objects up to store energy, then allowing their mass to fall and convert stored energy into kinetic energy for useful work. Electrical engineers design batteries and capacitors that store electric potential energy via separated positive and negative charges.

The mass-potential energy relationship also enables advances in renewable energy. For instance, pumped hydroelectric storage stations take advantage of the gravitational potential energy of water’s mass by pumping water uphill into reservoirs, then running it through turbines to generate electricity as it falls. The greater the water’s mass and height change, the more potential energy can be stored.

Even in chemistry, the mass of atoms relates to their potential energy levels and how they bond together. In general, the mass-potential energy connection applies widely across the sciences and engineering fields.

Limitations

While mass and potential energy generally have a direct relationship, there are some limitations and exceptions worth noting:

– The relationship only holds true in a uniform gravitational field. In a non-uniform field, the relationship becomes more complex.

– For gravitational potential energy, the relationship breaks down at speeds approaching the speed of light. Relativistic effects must be considered.

– For elastic potential energy, the relationship depends on the type of elastic material and how far it is stretched or compressed. The connection between mass and potential energy is not as straightforward.

– On a quantum scale, the nature of mass and potential energy changes. The direct proportionality between potential energy and mass no longer neatly applies.

– In systems with multiple interacting masses and energy transfers, it becomes difficult to isolate and quantify a simple relationship between mass and potential energy.

– The connection between mass and potential energy only applies to conservative force fields. In non-conservative fields with dissipative forces, friction, or energy losses, the relationship no longer holds.

– For complex systems like atoms and molecules, quantifying potential energy is challenging and depends on many factors beyond just mass.

So while mass and potential energy are generally directly proportional, the relationship has nuances, exceptions, and limits of applicability that are important to understand.

Conclusion

To summarize the key points about the relationship between mass and potential energy, there are a few main takeaways:

• Mass is directly related to potential energy – the greater the mass, the greater the potential energy.
• Gravitational potential energy increases with increasing mass, as gravity acts on the mass.
• Elastic potential energy also increases with greater mass, as more massive objects stretch or compress a spring more.
• This direct relationship allows potential energy to be calculated using mass, height, gravity, and other factors.
• Understanding the link between mass and potential energy helps explain real-world examples and applications.

In conclusion, mass and potential energy are intrinsically tied together through various equations and real-world systems. Their relationship demonstrates some key physics principles that are important to grasp.