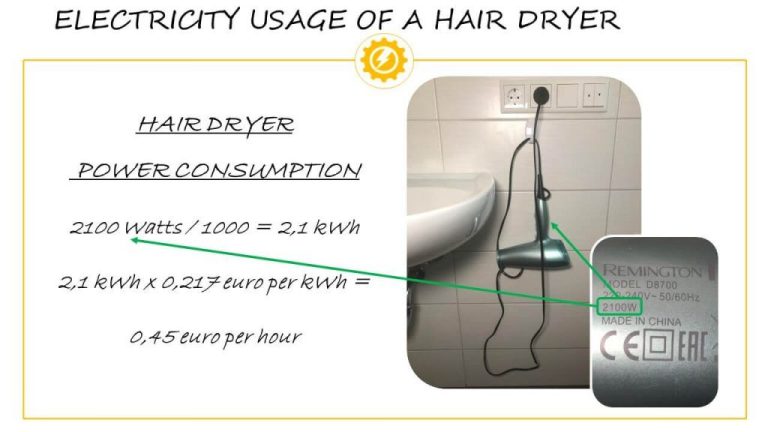
Which Points Are At The Same Potential?

Table of Contents

Definition of Potential

Electric potential is a measure of the amount of potential energy per unit charge at a specific location in an electric field. It is measured in volts and represents the amount of work needed to move a positive test charge from a reference point, often infinity, to that location without accelerating it.

Two points in an electric field are considered to be at the same potential if no work is required to move a test charge between them. This means that the test charge experiences no net force and does not gain or lose energy when moving between those two points. Even though the electric field may not be zero between the points, the work done by the electric force in one direction is equal and opposite to the work done against the force in the other direction, resulting in zero net work.

Electric potential energy is the potential energy stored in an object due to its electric charge and the electric field it experiences. It is directly proportional to the amount of charge and the potential at that point. When positive charges move from higher to lower potential, they lose electric potential energy, which can be turned into kinetic energy. The electric potential energy only depends on the potential difference between two points, not the path taken.

Measuring Potential

The potential difference between two points can be measured using a voltmeter. To measure potential difference, the voltmeter is connected across the two points in parallel. When current flows through the voltmeter, it indicates the potential difference on its scale.

An equipotential surface is an imaginary surface where every point has the same electric potential. No current flows between points on an equipotential surface since there is no potential difference. Equipotential surfaces are always perpendicular to the electric field lines. Drawing equipotential surfaces helps visualize the electric potential in a region of space.

To measure equipotential surfaces, two probes from a voltmeter are moved around the region. If the voltmeter reads zero volts between the probes, it indicates they are on the same equipotential surface. The readings can be recorded and plotted to map out the equipotential surfaces.

Points Connected by Conductor

When two points are connected by an ideal conductor, they are at the same electric potential. This is because conductors allow electric charges to flow freely. If two points on a conductor were at different potentials, it would create an electric field between those points that would cause current to flow until the potential difference was eliminated. Therefore, once equilibrium is reached, all points on a continuous conductor must be at the same electric potential.

For example, think about two metal spheres connected by a wire. If one sphere has a higher electric potential than the other, the electric field would drive electrons to flow from the higher potential sphere to the lower one. This flow of charge would continue until the spheres were at the same potential. At that point, the current stops because there is no longer a potential difference driving it. This demonstrates that conductively connected points equalize and reach the same electric potential.

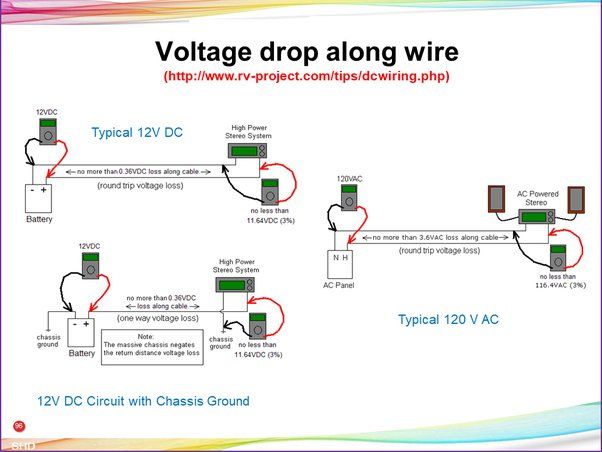
Points Not Connected

If two points are not connected by a conductive path, determining whether they are at the same potential requires analyzing the electric field between them. The electric field provides information about the voltage gradient, indicating how the potential difference changes from point to point.

Specifically, the change in potential between two points is equal to the negative integral of the electric field strength along a path connecting them. This is described mathematically by the equation:

ΔV = -∫E.dl

Where ΔV is the change in potential, E is the electric field, and dl is an infinitesimal segment along the path. If the integral evaluates to zero, it means the electric field is conservative and the potential difference between the start and end points is zero – they are at the same potential.

In physics, a conservative electric field means the work done in moving a charge between two points is independent of the path taken. So if the electric field is conservative, we can determine the potential difference between points A and B based solely on their positions, regardless of the path connecting them.

In summary, analyzing the electric field gradient between disconnected points provides the information needed to determine if they are at the same potential. The key is evaluating if the field is conservative, indicating zero potential difference.

Earth and Ground

Objects that are electrically connected to the earth are said to be “grounded.” The electrons in the earth distribute charges across it, making it neutral. When an object is connected to the earth through a conductor, excess charge will flow between the object and the earth until their electric potentials are equal. Since the potential of the earth is defined as 0 volts, the object’s potential will equalize to 0 volts as well. This is known as “grounding” an object.

Grounding is an important principle in electrical engineering and wiring. Sensitive electronics and electrical systems are often grounded to prevent build up of static charge and to safely direct excess current into the earth as a path of least resistance. By defining the earth to have 0 potential, it provides a reference point for measuring voltage in electrical circuits. Points in a circuit can then have positive or negative voltage relative to the zero earth ground.

So in summary, electrical systems or objects that are connected to the earth through conductors will equalize their potential to 0 volts. This grounding effect is useful for safety, static discharge, and providing a voltage reference point. Points at ground potential are at the same potential as the earth.

Electrostatic Equilibrium

Electrostatic equilibrium refers to the condition where there are no net electric fields or electric potentials within a system. This occurs when positive and negative charges are balanced so that their electric fields cancel out. Points that are at the same electric potential are considered to be in electrostatic equilibrium with one another.

When two points in space have the same electric potential, it means that no work would need to be done to move a positive test charge between those two points. The electric field strength between the points is zero. Therefore, there are no unbalanced forces acting on the test charge. This fulfills the condition of electrostatic equilibrium. Points at the same potential have equal amounts of potential energy, so the system remains stable.

The principle of electrostatic equilibrium explains why conductors can maintain an equipotential surface. When a conductor is exposed to external charges, its free electrons will redistribute until all points on the conductor reach the same potential. This allows conductors to shield contents from external electric fields. Electrostatic equilibrium is a key concept for understanding electric potential distributions.

Electric Potential Energy

The electric potential energy of a charged particle is the potential energy associated with the electric field. It’s energy that a charged particle gains from the electric field that it’s in.

We can derive an equation for the electric potential energy of a charged particle. Consider a charged particle with charge q in an electric field E. When the particle moves through a distance d in the field, it experiences a force F given by:

F = qE

The work done by the electric field in moving the charge is:

W = Fd = qEd

This work gets stored as potential energy of the charge. So the electric potential energy U is:

U = qEd

This shows that the potential energy of a charged particle in an electric field depends on its charge q and the electric field strength E. Charges with the same sign gain potential energy moving in the direction of the field, while charges with opposite signs lose potential energy.

Now consider two points at the same electric potential in a field. If a charge moves between these points, the work done on the charge by the field is zero since the points have the same potential. Therefore, the change in potential energy is also zero.

This demonstrates that the potential energy of a charged particle is the same at all points that have the same electric potential. The potential energy only depends on the potential, not the path taken.

Applications

The concept of points at the same potential has many important applications in physics and engineering. Here are some examples:

Electrostatics: In electrostatic systems like parallel plate capacitors, the two plates are kept at different potentials using a battery. This creates an electric field between the plates. However, the entire surface of each plate is at the same potential. This allows charge to distribute evenly on the plates.

Circuits: In electrical circuits, the points connecting any component are all at the same potential. This is known as a node. Analyzing circuits relies on identifying nodes and finding voltages between them. All points along a wire or component are at the same potential.

Nerve cells: The cell membrane of neurons maintains a voltage difference between the inside and outside of the cell. When a signal is transmitted, the potential rapidly changes at points along the membrane, allowing currents to flow to communicate information in the nervous system.

Visual Representations

Visual figures and diagrams can help illustrate the concept of electric potential in an intuitive way. Some examples include:

Equipotential lines mapping out areas of equal potential. These concentric lines are perpendicular to the electric field lines. Points along the same equipotential line are at the same potential.

Color gradients showing a continuous scale of electric potential values. Hot colors like red denote areas of high potential while cool colors like blue indicate lower potential regions.
3D surface plots visualizing the potential landscape for a system of charge distribution. Peaks and valleys correspond to areas of high and low electric potential respectively.

These types of visualizations make it easier to comprehend the invisible “topography” of electric potential that surrounds any charge configuration. They illustrate in a graphical manner how in electrostatics, nature always seeks to move charges from higher to lower potential.

Summary

In summary, two or more points in an electric circuit are considered to be at the same potential if they have an equal electric potential energy when no current is flowing between them. This occurs when the points are connected by an ideal conductor or are not part of a complete circuit. In these cases, the electrons can freely flow between the points and there is no voltage difference. Key takeaways include:

Points connected by a conductive path, like a wire, are at the same potential since charges can flow freely between them.
Points not connected as part of a circuit are at an ambiguous potential but can be considered at the same potential.

Earth or ground serves as a common reference point and can be used to determine if other points in a circuit share the same potential.
When charges stop flowing between points and reach electrostatic equilibrium, those points are at the same potential.

Understanding which points share the same potential helps predict current flow in circuits and utilize voltage properly in applications.