What Is Mechanical Energy The Sum Of And Object’S?
Mechanical energy is the sum of an object’s kinetic energy and potential energy. It is a fundamental concept in physics and engineering that describes the capacity for an object or system to do work based on motion and position.
Mechanical energy provides a quantitative way to characterize phenomena we observe every day – things like a ball rolling down a hill, a book sitting on a table, or a bicycle in motion. The mechanical energy present in these systems enables them to do useful work like accelerating, lifting objects, or powering machines.
For example, a swinging pendulum has kinetic energy at the bottom of its arc from its motion, and potential energy at the top of its arc from its elevated position. The total mechanical energy remains constant as the pendulum swings back and forth, transforming between kinetic and potential.
Understanding mechanical energy is crucial for describing and predicting the behavior of physical systems across many scientific and engineering fields. It is a fundamental building block in topics like dynamics, thermodynamics, and mechanics.
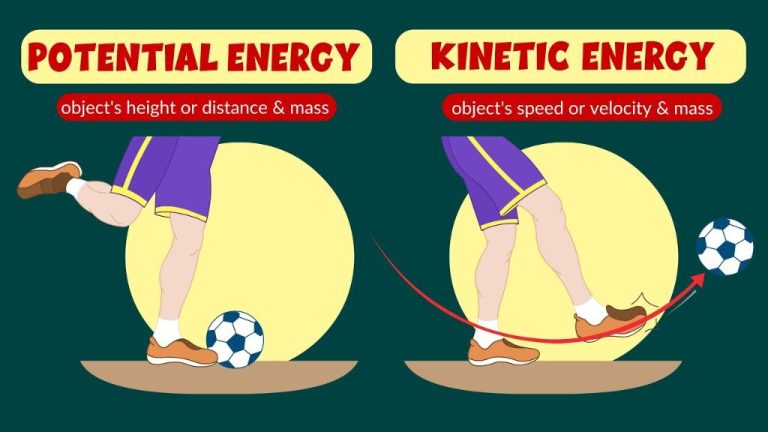
Kinetic Energy
Kinetic energy is the energy an object possesses due to its motion. It depends on two physical quantities – the mass (m) and velocity (v) of the object. The kinetic energy (KE) of an object can be calculated using the following equation:
KE = 1/2 * m * v^2
Where m is the mass of the object in kilograms (kg) and v is its velocity in meters per second (m/s). This shows that an increase in either mass or velocity will result in an increase in the object’s kinetic energy. Doubling the mass, for example, doubles the kinetic energy. However, doubling the velocity results in a four-fold increase in kinetic energy. This relationship explains why high-velocity objects like bullets have tremendous kinetic energy even if they are small in mass.
Kinetic energy is a form of mechanical energy present in all moving objects. Understanding how an object’s mass and velocity determine its kinetic energy provides insight into physics and mechanics. This concept has many important real-world applications in fields like engineering, transportation, sports science and more.
Potential Energy
Potential energy is the energy stored in an object or system due to its position or configuration. There are different types of potential energy depending on the forces involved:
- Gravitational potential energy – This depends on an object’s height above the ground, or distance above some other object that is exerting a gravitational force on it. The higher the position, the greater the gravitational potential energy.
- Elastic potential energy – Stored in elastic materials or objects that are deformed or compressed. The more an elastic object is stretched or compressed, the greater its elastic potential energy.
- Chemical potential energy – Stored in the chemical bonds between atoms and molecules. Chemical reactions can release this potential energy.
- Nuclear potential energy – Stored in the binding forces within an atomic nucleus. Nuclear reactions like fission and fusion can release nuclear potential energy.
In general, potential energy depends on the position, shape, or configuration of an object within a force field. A compressed spring has more potential energy than a relaxed spring. A book on a high shelf has more gravitational potential energy than the same book on the floor. The key point is that potential energy is not based on motion or kinetics, but rather on an object’s position or structure.
Conservation of Mechanical Energy
One of the most important laws governing mechanical energy is the law of conservation of energy. This law states that in a closed system, the total mechanical energy remains constant. The mechanical energy cannot be created or destroyed – it can only be transformed from one form into another.
For example, consider a ball rolling down a ramp. At the top of the ramp, the ball has potential energy due to its elevated position in the gravitational field. As the ball rolls down the ramp, this potential energy gets converted into kinetic energy, increasing the velocity of the ball. However, the total mechanical energy – the sum of potential and kinetic energy – remains the same throughout the motion.
Another example is a pendulum swinging back and forth. At the extremes of its swing, it has maximum potential energy and zero kinetic energy. At the lowest point, it has maximum kinetic energy and zero potential energy. But the total energy remains constant. Friction and other dissipative forces may decrease the total mechanical energy over time, but in an ideal frictionless system, the total mechanical energy is always conserved.
This law is extremely useful in analyzing mechanical systems. By tracking the energy transfers between potential and kinetic forms, the total energy can be calculated at any point. Conservation of mechanical energy is a foundational concept across physics and engineering.
Mechanical Energy in Simple Machines
Simple machines like levers, pulleys, gears, and inclined planes allow us to transform mechanical energy to do work in an easier or more efficient way. For example, a lever transforms the direction or magnitude of a force applied to one end into a different force applied to another end to lift an object. The mechanical energy remains the same, but the lever makes it easier to do work by changing the amount of force needed.
A pulley utilizes ropes and wheels to change the direction of an applied force to lift an object. More complex pulley systems with multiple wheels and ropes allow us to apply less force to lift the same load. Again, mechanical energy is conserved but transformed into different forces and distances through the pulley system.
Gears connect to increase or decrease rotational speed and torque. In this way, gears transform forces and motion to allow a small applied force to turn a large gear. The mechanical energy remains constant while the gears trade off force and distance.
Inclined planes transform a force applied over a shorter distance into a force over a longer distance. Less force is needed on an inclined plane to raise an object than lifting it straight up. The mechanical energy stays the same while the ramp does the work of transforming the force.
Understanding how simple machines transform mechanical energy while following the law of conservation of energy helps explain how they provide a mechanical advantage to do work more easily. This is a key application of mechanical energy principles.
Mechanical Energy in Real-World Systems
Mechanical energy is present in many real-world systems that we encounter every day. Here are some examples:
Vehicles: Cars, trucks, trains, and other vehicles have kinetic energy when they are moving. The faster they move, the more kinetic energy they have. They can convert this kinetic energy into potential energy by driving up a hill. As they go higher up the hill, their potential energy increases. When they drive back down, the potential energy is converted back into kinetic energy.
Roller coasters: Roller coasters have kinetic and potential energy. As they go downhill, they gain speed and kinetic energy. As they go uphill, they trade kinetic energy for potential energy. At the top of a hill, their potential energy is at a maximum. Rolling downhill converts this potential back into kinetic energy.
Springs and bungees: Springs and bungee cords store potential energy when stretched or compressed. As the stretched spring is released, the potential energy converts into kinetic energy. The spring can go back and forth between potential and kinetic energy until friction dissipates the energy.
Pendulums: Pendulums convert between kinetic and potential energy. At the lowest point, they have maximum kinetic energy. At the highest point, they have maximum potential energy. The interchange between kinetic and potential happens with each swing.
There are many more examples of mechanical energy conversions happening in the world around us. Recognizing these energy transfers helps us better understand the physics at work in everyday systems.
Calculating Mechanical Energy
Mechanical energy is calculated by adding together an object’s kinetic energy and potential energy at any given moment. Here is the equation:
Mechanical Energy = Kinetic Energy + Potential Energy
Kinetic energy (KE) is energy associated with motion and is calculated using the equation:
KE = 1/2 * m * v^2
Where m is the mass of the object and v is its velocity.
Potential energy (PE) is stored energy due to an object’s position or state. The equation for gravitational potential energy is:
PE = m * g * h
Where m is mass, g is the gravitational acceleration constant, and h is the height of the object.
By adding KE and PE together at any given point, you can calculate the total mechanical energy of an object or system. This is a useful concept for analyzing mechanical systems across many fields such as physics, engineering, and architecture.
Applications and Significance
Mechanical energy is a fundamental concept in physics and engineering that has many important real-world applications. Understanding mechanical energy is crucial for designing and analyzing mechanical systems, ranging from simple machines like levers and pulleys to complex systems like vehicles, robots, and manufacturing equipment.
The principles of mechanical energy allow engineers to predict how components like springs, gears, and motors will behave under various conditions. This knowledge is applied when determining how to store, transfer, and convert energy in machines to perform useful work efficiently and safely.
Devices like rollercoasters and elevators rely heavily on conversions between gravitational potential energy and kinetic energy. The mass and velocity of moving parts must be carefully calculated to ensure proper operation. Mechanical energy concepts also help optimize renewable energy systems that harness wind, water, or solar power.
In addition, knowledge of mechanical energy aids in preventing and mitigating disasters. For example, calculating the kinetic energy involved in collisions allows automotive engineers to design effective braking systems and protective features like airbags and crumple zones. Proper analysis of the potential energy in raised weights or pressurized containers helps identify risks and prevent accidents in industrial settings.
By providing a quantitative understanding of how energy is transferred and converted in mechanical processes, the principles of mechanical energy enable the design and optimization of countless important technologies that impact quality of life across many fields. Mechanical energy is a foundational physics concept with broad relevance and applicability in the modern world.
Common Misconceptions
There are several common misconceptions people have about mechanical energy:
Thinking mechanical energy is not conserved – Many believe that mechanical energy is “lost” or disappears, but according to the law of conservation of energy, mechanical energy is never lost but simply transformed into other forms of energy like heat, sound, etc.
Confusing mechanical energy and kinetic energy – Mechanical energy is the sum of kinetic and potential energy, whereas kinetic energy is just the energy of motion. Potential energy exists even when objects are not moving.
Assuming mechanical energy is only for mechanical/physical systems – While the term implies machines and mechanics, mechanical energy applies to all objects that have kinetic or potential energy, including chemical and thermal systems.
Believing mechanical energy applies to non-conservative forces – Mechanical energy is only conserved when forces are conservative. It does not apply to non-conservative forces like friction which dissipate energy as heat.
Thinking an object at rest has no mechanical energy – A stationary object can still possess potential energy due to its position or composition. Mechanical energy requires motion (kinetic) or the potential for motion.
Confusing units used to measure mechanical energy – Kinetic energy is measured in Joules, potential energy is measured in Joules, but mechanical energy is measured in Joule-Newtons or simply Newtons.
Not realizing how prevalent mechanical energy is – From bouncing balls to rollercoasters to wind-up toys, mechanical energy is found almost everywhere in our daily lives.
Summary
Mechanical energy is the sum of an object’s kinetic energy and potential energy. Kinetic energy is the energy an object has due to its motion. Potential energy is stored energy due to an object’s position or configuration. The principle of conservation of mechanical energy states that in an isolated system with no outside forces, the total mechanical energy remains constant. Mechanical energy can be transferred between kinetic and potential forms, such as in the operation of simple machines like ramps, levers, and pendulums. The mechanical energy in real-world systems gets dissipated into other forms like heat and sound due to friction and non-conservative forces. Mechanical energy is calculated by adding the kinetic and potential energy. Understanding mechanical energy helps predict system behavior and improve efficiency in fields like engineering and physics. While the total mechanical energy is conserved, some of it inevitably gets converted to thermal energy, so perpetual motion machines are impossible.