Do Planets Have Kinetic Energy?
Kinetic energy is defined as the energy an object possesses due to its motion. It depends on the mass and velocity of an object and is calculated using the formula KE = 1/2mv^2, where m is mass and v is velocity (https://byjus.com/physics/kinetic-energy/). Kinetic energy is an important concept when discussing planets because planets are constantly in motion, orbiting around stars or other planetary bodies. As celestial objects move through space, they possess kinetic energy that interacts with the gravitational fields they encounter. Understanding kinetic energy is key to explaining planetary orbits, motions, and interactions within solar systems.
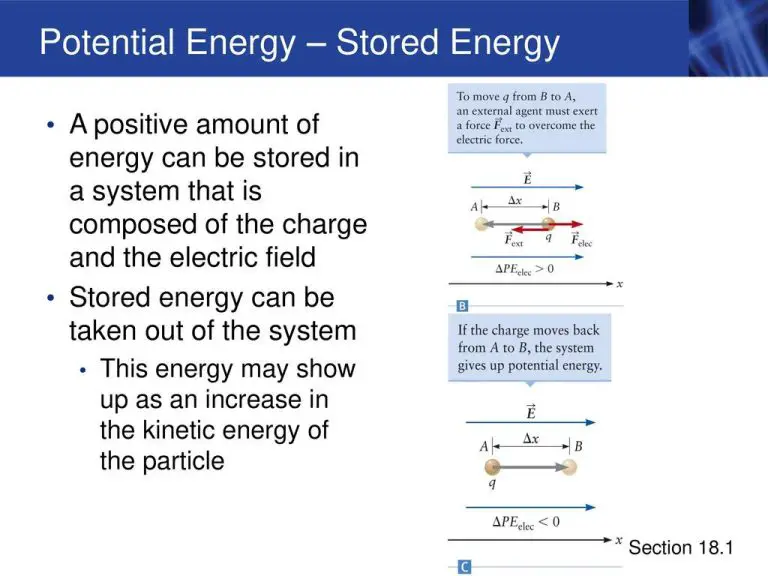
Kinetic energy is often contrasted with potential energy, which is the stored energy an object has due to its position or configuration (https://www.merriam-webster.com/dictionary/kinetic%20energy). The motions and configurations of celestial objects like planets involve conversions between kinetic and potential energy, so both concepts are essential for modeling astrophysical processes. Kinetic energy contributes to the stability of planetary orbits over time. It also plays a role in tidal forces, planetary collisions, and other energetic phenomena on a cosmic scale.
In summary, kinetic energy is a fundamental property of moving objects like planets. Quantifying and tracking this kinetic energy is critical for understanding the mechanics of our solar system and the universe.
The Motion of Planets
Planets are constantly in motion as they orbit the sun and rotate on their axes. According to NASA, planets orbit the sun in ellipses, with the sun at one focal point of the ellipse (NASA: Orbits and Revolutions). Though early astronomers believed planets moved in perfect circles, Johannes Kepler discovered in the 17th century that the orbits are elliptical, with the sun offset from the center (Science Learning Hub). The speed of a planet’s orbital motion depends on its distance from the sun as described by Kepler’s second law of planetary motion.
In addition to orbiting the sun, planets rotate on their axes at varying speeds. For example, Jupiter has a rotational period of just under 10 hours, completing a full rotation every 9 hours and 56 minutes. In contrast, Venus rotates very slowly, with its day lasting 243 Earth days – longer than its year of 225 days! This combination of orbital revolutions and axial rotations keeps the planets in constant motion.
Kinetic Energy Formula
The formula for kinetic energy is:
KE = 1/2 * m * v2
Where:
- KE is the kinetic energy in joules (J)
- m is the mass of the object in kilograms (kg)
- v is the speed of the object in meters per second (m/s)
This formula shows that an object’s kinetic energy depends on both its mass and its velocity squared. The faster an object moves, the more kinetic energy it has. Doubling the velocity results in a quadrupling of the kinetic energy. The greater the mass, the greater the amount of energy required to accelerate it.
Kinetic energy is directly proportional to mass and to the square of velocity. This means that an object with more mass, or that is moving faster, has greater kinetic energy.
Applying the Formula to Planets
The basic formula for kinetic energy is:
Kinetic Energy = 1/2 x mass x velocity squared
We can apply this formula to planets in our solar system to demonstrate that yes, planets do possess kinetic energy due to their orbital motion around the sun. For example, let’s calculate the kinetic energy of the Earth:
Mass of Earth = 5.972 x 10^24 kg
Average orbital velocity of Earth = 29,783 m/s
Plugging into the formula:
KE = 0.5 x 5.972 x 10^24 kg x (29,783 m/s)^2
= 2.67 x 10^33 J
This shows that the Earth has tremendous kinetic energy due to its orbital motion. We can do similar calculations for other planets as well. The kinetic energy possessed by planets is one reason why space missions require so much energy to leave Earth’s orbit. Overcoming a planet’s kinetic energy is a key challenge for space travel.
In summary, by applying the kinetic energy formula it is clear that yes, planets do have very large amounts of kinetic energy due to their motion around the sun and through space.
Other Sources of Kinetic Energy
While a planet’s orbital motion around the sun is the primary source of its kinetic energy, planets can gain additional kinetic energy from other forms of motion. For example, planets that have moons gain kinetic energy from the motion of those moons orbiting around them. The formula for kinetic energy depends on the mass and velocity of the object. So the mass of the moon and its orbital velocity around the planet contribute additional kinetic energy to the planet-moon system.
As an example, the Earth gains kinetic energy not just from its own orbit around the sun, but also from the motion of its moon. The moon has a mass of 7.34 x 10^22 kg and orbits the Earth at an average velocity of 1.023 km/s. Plugging this into the kinetic energy formula shows the moon contributes 2.36 x 10^29 Joules of additional kinetic energy beyond the Earth’s own orbital motion. This added kinetic energy affects things like tides on Earth.
Other planets with multiple moons, like Jupiter and Saturn, gain even more kinetic energy from the motions of their moons around them. So a planet’s total kinetic energy depends not just on its own orbit, but also on the motions of its moons, which can be a significant addition.
Converting Potential Energy
Planets can convert potential energy into kinetic energy through gravitational interactions. As a planet orbits the sun, it has gravitational potential energy due to its position in the gravitational field. This potential energy can be converted into kinetic energy as the planet falls towards the sun. The conversion between potential and kinetic energy allows planets to remain in orbit.
According to Energy in Orbits, “As a planet orbits further away from the Sun, the increase in gravitational potential energy is balanced by the decrease in kinetic energy.” The gravitational pull of the sun causes the planet to accelerate and speeds it up. This increase in velocity corresponds to an increase in kinetic energy. At the same time, as the planet gets closer to the sun, it loses gravitational potential energy. The total mechanical energy remains constant, but transformation between potential and kinetic energy allows continued orbital motion.
Impact on Orbits
Kinetic energy plays an important role in determining the orbits and motions of planets. According to the law of conservation of energy, the total mechanical energy of a planet, consisting of kinetic and potential energy, remains constant as it orbits the Sun. Kinetic energy increases as a planet speeds up and decreases as it slows down. Potential energy works inversely – increasing as a planet moves away from the Sun and decreasing as it gets closer.
For objects in circular orbits like planets, kinetic and potential energy are balanced. As a planet travels away from the Sun, its potential energy rises while its kinetic energy drops by the same amount. When the planet is closest to the Sun, it has maximum kinetic energy and minimum potential energy. This exchange between kinetic and potential energy allows planets to remain in stable orbits.
For elliptical orbits, the math is more complex but the principle remains the same. Kinetic energy is highest at the closest point (perihelion) and lowest at the farthest point (aphelion). The shape and orientation of a planet’s orbit depend on its total mechanical energy as well as its angular momentum.
Changes in a planet’s kinetic energy over time, caused by interactions with other objects, can alter its orbit. Increased kinetic energy makes the orbit less circular, while decreased kinetic energy makes it more circular. Kinetic energy is crucial for understanding how planets move through space around their parent stars.
Astrophysical Significance
Kinetic energy is a crucial concept in astrophysics and for understanding our solar system. The motion of celestial bodies like planets, moons, asteroids, and comets depends on their kinetic energy [1]. These objects have kinetic energy due to their orbital motion around the Sun or other bodies. This motion allows astronomers to calculate their kinetic energy using the formula: Kinetic Energy = 0.5 x Mass x Velocity^2.
Kinetic energy explains how planets maintain stable orbits and why some asteroids and comets have erratic paths. Objects with more kinetic energy in their orbits are harder to deflect onto different trajectories. Gravity provides the centripetal force to circularize orbits, while kinetic energy resists changes. Astronomers can model the evolution of our solar system and probe its history by analyzing the kinetic energy of bodies over time [2].
Kinetic energy conversions also power astronomical phenomena. The gravitational potential energy of infalling matter gets converted into kinetic energy, heating up accretion disks around black holes. This emitted radiation allows astronomers to detect black holes. Supernova explosions are similarly fueled by such energy conversions. Overall, kinetic energy is integral to motion in space and many processes studied in astrophysics.
Kinetic Energy Over Time
The kinetic energy of planets does not change significantly over astronomical timescales. While planets do lose some kinetic energy over time due to tidal effects and gravitational interactions, these changes are negligible on human timescales.
For example, the Earth’s orbital velocity changes by only about 1 meter per second every 50,000 years. This is an extremely small change compared to its average orbital velocity of 30 kilometers per second. Over billions of years, the cumulative effect may add up, but the kinetic energy remains relatively stable on timescales relevant to human civilization.
Other effects like tidal forces between the Earth and Moon and interactions with other planets impart very minor perturbations. But the planets follow approximately fixed elliptical orbits over very long periods. According to Kepler’s Laws, without any external forces, planets would continue orbiting the Sun indefinitely. Their kinetic energy is nearly constant when averaging over geological epochs.
So in summary, while some minute gains and losses occur, the kinetic energy of the planets around the Sun remains remarkably fixed over astronomical timescales. Only over billions of years do cumulative effects start to impact the orbital parameters.
Conclusion
In summary, the answer to the original question “Do planets have kinetic energy?” is definitively yes. Planets orbiting stars possess both rotational kinetic energy from spinning on their axes, as well as orbital kinetic energy from revolving around the star. The kinetic energy of planets can be calculated using the standard formula for kinetic energy, KE = 1/2mv^2. As planets orbit their stars, they continuously convert between kinetic and potential energy, with kinetic energy highest at the closest point to the star. While kinetic energy varies over a planet’s orbit and rotation, the total mechanical energy remains constant if no external forces act on it. Understanding planetary kinetic energy provides astrophysicists insights into the nature of orbits and how gravitational forces govern motion in our solar system and beyond.