What Is Electrical Energy In Physics?
Electrical energy is the energy carried by charged particles such as electrons and protons. It is a form of energy resulting from the movement of electrically charged particles. When charges move through conductive materials such as wires and circuits, electrical energy gets transferred from one place to another.
Some key basics about electrical energy include:
- It results from the flow of electric charge – the movement of electrons
- The charge flows when there is a voltage – a difference in electric potential
- The greater the voltage, the stronger the electric field created to move the charges
- The charges move through conductive paths like metal wires and cables
- This flow and transfer of electric charge is called electricity
Electrical energy is an extremely useful and versatile form of energy in modern society. Some of its important applications and uses include:
- Powering electrical devices and appliances in homes and buildings
- Long distance transmission of power from generating stations to substations
- Powering motors, machinery, and industrial processes
- Powering communications networks and IT infrastructure
- Battery storage in portable consumer electronics and electric vehicles
In summary, electrical energy involves the flow of electric charges and is critical for modern power generation, transmission, and use. It powers the technologies and infrastructure of industrial societies.
Electric Potential Energy
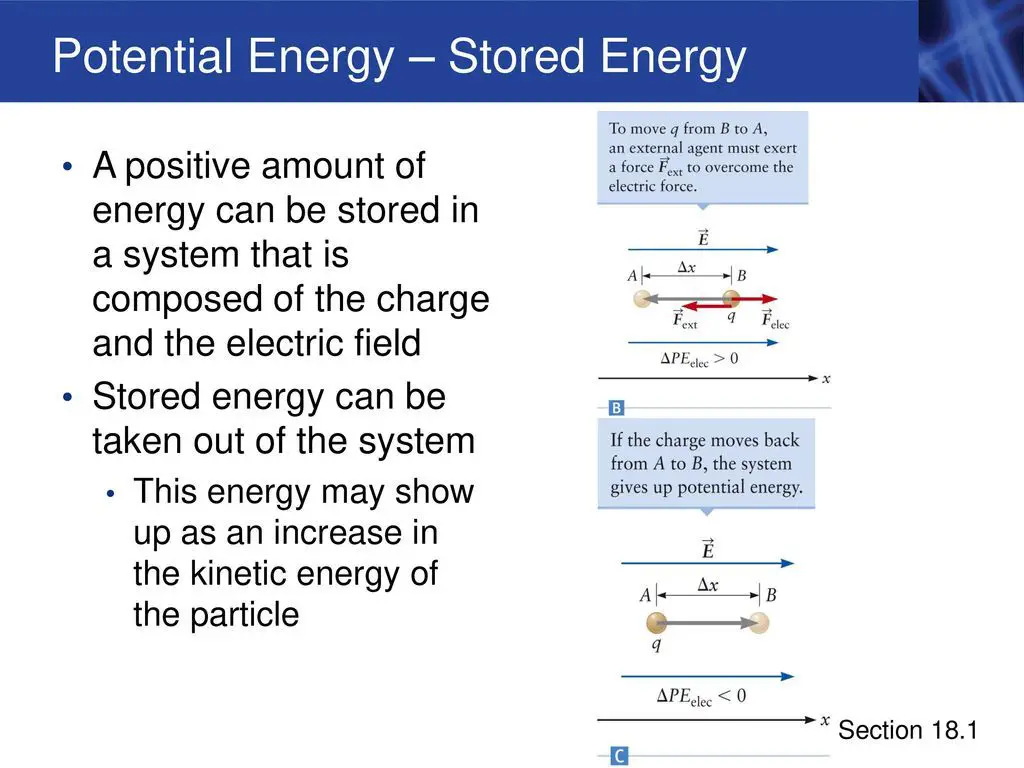
Electric potential energy refers to the potential energy stored in an electric field or system of charges. It is the energy possessed by charged particles by virtue of their electric charge and relative positions in an electric field. The main factors that determine electric potential energy are:
- The amount of electric charge (Q)
- The electric potential (V)
The standard unit for electric potential energy is the joule (J). The electric potential energy stored in a system of charges is directly proportional to the amount of charge and the voltage or electric potential. This relationship can be represented by:
Electric Potential Energy = Q x V
Where Q is the electric charge in coulombs (C) and V is the voltage or electric potential in volts (V). So the greater the amount of charge and higher the voltage, the more potential energy stored.
Some examples of systems that store electric potential energy include:
- Capacitors – Store potential energy in the electric field between their plates.
- Batteries – Chemical reactions produce separated electric charges that possess potential energy.
- Generators – Convert mechanical energy into electric potential energy.
This potential electric energy can be converted into other forms of energy like kinetic, light, or thermal energy when electric charges are allowed to flow through a circuit. Understanding electric potential energy is key to electrical engineering and harnessing electricity.
Electric Field Energy
Electric field energy refers to the energy stored in an electric field due to the positions of charged particles. It arises from the interactions between positively and negatively charged particles. Specifically, work must be done to assemble positive and negative charges into a configuration where they produce an electric field. This work done is stored as electric potential energy.
The electric field itself stores energy by virtue of its ability to exert forces on charged objects. The electric potential energy stored in the field is proportional to the electric field strength. The units of electric field energy density are joules per cubic meter (J/m3).
The relationship between electric field and potential energy can be described mathematically. The electric potential energy density u stored in an electric field E is given by:
u = (1/2)ε0E2
Where ε0 is the electric constant. This shows that the energy density is proportional to the square of the electric field strength. In regions where the electric field is stronger, more energy is stored per unit volume.
Capacitors and Electrical Energy Storage
Capacitors are devices that can store electric energy. When the capacitor is charged by connecting it to a power source, charge builds up on each of its plates and creates an electric field between them. The energy stored in a capacitor is proportional to the square of the electric charge on the plates according to the equation:
E = (1/2)CV2
Where C is the capacitance, a measure of the capacitor’s ability to store charge for a given voltage, and V is the voltage across the capacitor. Some key factors that affect a capacitor’s storage capacity include:
- Plate Area – Larger plate area means more charge can be stored for a given voltage.
- Plate Separation – Smaller separation between the plates means greater capacitance and more charge storage.
- Dielectric Material – Materials with higher permittivity allow more charge to be stored.
Capacitors are often used in electric circuits and electronic devices to store electric energy for high-power applications. Their ability to rapidly charge and discharge makes them ideal for energy storage in camera flashes, defibrillators, and other pulse power supplies.
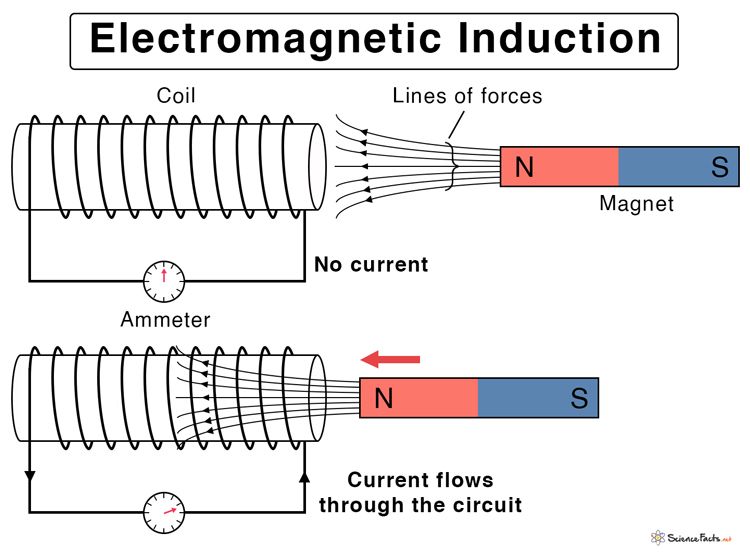
Magnetic Energy
Magnetic energy is the energy stored in a magnetic field. It is the potential energy of a magnetic system. The SI unit of magnetic energy is the joule (J).
The magnetic energy stored in a magnetic field depends on the strength of the magnetic field and the volume of space occupied by the field. The larger the volume containing the magnetic field and the stronger the magnetic field, the greater the magnetic energy stored.
The most common source of magnetic fields is an electromagnet, which consists of a coil of wire with an electric current running through it. The magnetic energy stored in the electromagnet’s magnetic field is proportional to the square of the current flowing in the coil and the inductance of the coil. The inductance depends on the number of turns in the coil and the material inside the coil. More turns and a ferromagnetic core material (such as iron) inside the coil result in higher inductance and greater magnetic energy storage.
Permanent magnets also contain magnetic energy stored in their magnetic fields. The stronger the permanent magnet (higher magnetic flux density or field strength), the greater the volume of the magnet, and the greater the magnetic energy stored.
In both electromagnets and permanent magnets, the magnetic energy comes from the magnetic dipoles (tiny north and south magnetic poles) aligning their magnetic moments with the external magnetic field. This alignment against the randomized thermal motion requires energy, which is then stored in the magnetic field.
Electrical Current and Energy Transfer
Electric current involves the flow of charged particles, such as electrons, through a conducting material. Therefore, the current flowing through a conductor is related to how much energy is being transferred through that conductor. The relationship can be understood using the following equation:
Power (P) = Current (I) x Voltage (V)
Power represents the rate at which energy is transferred. Current is the rate of flow of charge. Voltage can be thought of as the “push” that causes the charges to flow. So in this equation, the current and voltage affect how quickly energy gets transferred through the conductor.
There are two main factors that affect the rate of energy transfer in an electrical current:
- Resistance – Materials like metal wires tend to resist the flow of current. The more resistant a material is, the lower the current will be for a given voltage. Since power depends on current, higher resistance in a conductor will reduce the rate of energy transfer.
- Voltage – The higher the voltage, the stronger the “push” on the charges in the conductor. This increased driving force causes more current to flow, which increases the rate of energy transfer.
Therefore, to maximize the rate of energy transfer through a conductor, the resistance should be low and the voltage high. This is why high voltage transmission lines are used to transfer large amounts of electrical power efficiently over long distances.
Electrical Power
Electrical power is defined as the rate at which electrical energy is transferred. The standard SI unit for power is the watt (W). Power describes how quickly energy is being used or produced within an electrical circuit.
Power is related to both current and voltage in a circuit. The relationship is described by:
P = IV
Where P is power (in watts), I is current (in amps), and V is voltage (in volts). This equation shows that power increases proportionally with current and voltage. Doubling either the current or voltage in a circuit doubles the power.
Power can also be calculated using:
P = I2R = V2/R
Where R is the resistance (in ohms). This further demonstrates the direct relationship between power and current or voltage.
Understanding electrical power is important for properly designing and operating electrical devices and systems. Calculating power consumption allows proper sizing of power sources, conductors, and system components.
Direct Current Circuits
Direct current (DC) circuits involve current flowing in one direction through circuit elements. Some key principles for analyzing DC circuits include:
Ohm’s Law
Ohm’s law states that the current through a conductor is directly proportional to the voltage across it. This relationship is given by:
V = IR
Where V is voltage, I is current, and R is resistance. This law shows that increasing voltage across a fixed resistor will increase the current through it.
Series vs. Parallel Circuits
In a series circuit, current passes through each component in a single loop. The current stays the same but voltage drops across each resistor. In a parallel circuit, current branches off through each component. The voltage stays the same but current divides among each branch.
Electrical Power
Power in a DC circuit is given by:
P = IV
Where P is power, I is current, and V is voltage. Power is related to the rate of energy transfer and can also be calculated using resistance as:
P = I2R = V2/R
Increasing current or voltage will increase the power dissipated in a resistor.
Analyzing these relationships allows calculation of power, current, voltage, and resistance in DC circuit analysis.
Alternating Current and Electrical Energy
Alternating current (AC) is a type of electrical current where the flow of electric charge periodically reverses direction. The voltage driving an AC circuit also varies periodically in a sinusoidal pattern. In contrast, direct current (DC) flows in only one direction with a constant voltage.
AC is used in power distribution because it allows voltage levels to be increased or decreased easily with transformers. This allows efficient transmission over long distances. Most household plugs and outlets provide AC power.
The rate at which AC voltage changes polarity is called the frequency, measured in Hertz (Hz). Standard AC power grids operate at 60 Hz in North America and 50 Hz in Europe, Asia, Africa and Australia.
Due to the changing polarity of AC power, concepts like electrical impedance and reactance become important. Impedance is like resistance, but accounts for both the resistive and reactive properties of a load. It represents the total opposition to AC current flow.
For resistors, impedance is equivalent to resistance. But components like inductors and capacitors exhibit reactance that varies with the AC frequency. AC analysis uses complex numbers to handle calculations involving magnitude and phase.
AC power is calculated using formulas like:
Power (P) = Voltage (V) x Current (I) x Cosine (phi)
Where phi is the phase angle between voltage and current.
Transformers consist of two coils that transfer energy from one AC circuit to another with different voltage levels. By stepping voltage up and down, AC power can be transmitted efficiently over long distances before being reduced to lower levels for consumer use.
AC motors, generators, and other appliances all rely on the principles of alternating current and voltage to function. Though more complex than DC, AC provides flexibility in generation, transmission, distribution and end-use applications.
Applications of Electrical Energy
Electrical energy powers many essential devices, systems, and infrastructure in our daily lives. Here are some examples of how we utilize electrical energy:
Lighting: Electricity allows us to illuminate homes, workplaces, streets, and cities with light bulbs, neon signs, and other lighting fixtures.
Appliances: Common household appliances like refrigerators, microwaves, washing machines, and air conditioners all run on electrical energy.
Electronics: Laptops, cell phones, televisions, gaming systems and other electronics need electricity to operate and charge their batteries.
Heavy Industry: Factories use large amounts of electrical power for manufacturing, operating heavy machinery, and automation processes.
Infrastructure: Mass transportation systems like subways, railways, and electric buses rely on electricity to run and operate signals, controls and Displays.
Medical Technology: Electricity powers vital medical equipment like X-ray machines, MRI scanners, and life support systems in hospitals.
Computing: Data centers, supercomputers, and server farms require massive amounts of electrical energy to process and store data.
In summary, modern civilization depends heavily on harnessing electrical energy for illumination, industry, transportation, infrastructure, technology and more. Our daily lives would look very different without all the applications of electrical power around us.