What Is Mechanical Energy Determined By?

Mechanical energy is the energy associated with motion and the arrangement of objects and substances. It is the sum of kinetic energy and potential energy in a system. Mechanical energy is ubiquitous in our everyday lives and is involved in almost everything we do.

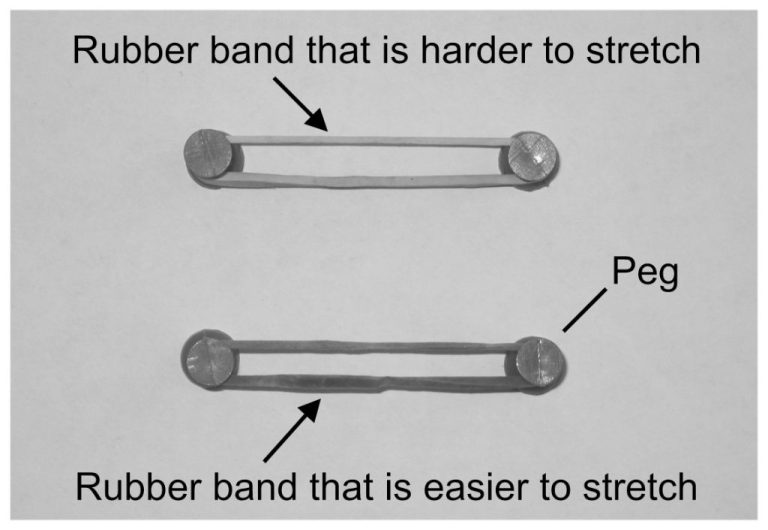
For example, a rollercoaster moving along its tracks has mechanical energy due to its motion. A stretched rubber band has mechanical energy stored in it due to its deformation. Even something as simple as a book sitting on a table contains mechanical energy because of its position in relation to the ground.

Mechanical energy can be converted into other forms of energy like electrical energy, heat, light, and sound. Engines, generators, speakers, and light bulbs are some common examples of devices that convert mechanical energy into other forms.

Understanding mechanical energy is crucial in fields like physics, engineering, architecture, construction, and more. The principles of mechanical energy enable us to build and operate machines, vehicles, infrastructure and much of the modern world.

Kinetic Energy

Kinetic energy is the energy of motion. An object that has motion – whether it is vertical or horizontal motion – has kinetic energy. The amount of kinetic energy an object has depends on two variables: mass and velocity.

The formula for kinetic energy is:

Kinetic Energy = 1/2 x Mass x Velocity^2

Where mass is measured in kilograms (kg) and velocity is measured in meters per second (m/s). The kinetic energy is measured in Joules (J).

Some examples of kinetic energy in everyday life include:

• A moving car
• A soccer ball being kicked
• Wind blowing
• A bicycle being ridden

In each of these examples, the object in motion has kinetic energy proportional to its mass and the square of its velocity.

Potential Energy

Potential energy is the stored energy an object has due to its position or shape. There are several types of potential energy:

• Gravitational Potential Energy – This is energy stored due to an object’s height relative to the ground in a gravitational field. The formula for gravitational potential energy is:

PE_grav = mgh

Where m is mass, g is gravitational acceleration, and h is height. For example, a book sitting on a high shelf has more gravitational potential energy than when it is sitting on a low shelf.

• Elastic Potential Energy – This is energy stored in elastic objects that are deformed. For example, a stretched rubber band has elastic potential energy.
• Chemical Potential Energy – This is energy stored in the bonds between atoms and molecules. Food and fuel both contain chemical potential energy that can be released through chemical reactions.

In summary, potential energy depends on an object’s configuration and is converted into kinetic energy when released.

Conservation of Mechanical Energy

The law of conservation of mechanical energy states that in an isolated system that is not subject to any external forces, the total amount of mechanical energy remains constant. Mechanical energy cannot be created or destroyed, only converted between different forms. The two main forms of mechanical energy are kinetic energy and potential energy.

Kinetic energy is the energy an object possesses due to its motion. Potential energy is stored energy that depends on an object’s position or shape. In real world systems, mechanical energy can readily transform back and forth between kinetic and potential energy.

For example, a ball at the top of a ramp has potential energy due to its elevated position in the gravitational field. As the ball rolls down the ramp, this potential energy gets converted to kinetic energy, increasing the ball’s speed. At the bottom of the ramp, the ball has maximum kinetic energy and minimal potential energy. If the ball then travels upwards onto another ramp, the kinetic energy gets converted back into potential energy as it gains elevation.

According to the law of conservation of mechanical energy, the total amount of mechanical energy in such a system remains constant. Energy is never lost, but simply transformed from one form to another. This law applies to any isolated system with conservative forces like gravity. Understanding the conservation of mechanical energy is crucial for analyzing mechanical systems across physics and engineering.

Work

Work is an important concept in physics that is closely related to energy. In physics, work refers to the energy transferred when a force acts on an object, causing it to move in the direction of the force. Work is said to be done when the force applied causes the object to be displaced or move.

According to the work-energy theorem, the net work done on an object is equal to its change in kinetic energy. This means that if net work is done on an object, its kinetic energy will change by the same amount. For example, if a net force of 10 Newtons pushes an object 5 meters, 50 Joules of work is done on the object. This will cause the object’s kinetic energy to increase by 50 Joules as well.

The work-energy theorem is based on the law of conservation of energy and helps explain how mechanical energy is transferred from one form (work) to another (kinetic energy). It shows the direct relationship between work and changes in kinetic energy for objects upon which external forces are acting.

Power

Power is defined as the rate at which work is done or energy is transferred. It is calculated as work divided by time.

The relationship between work and power is an important one. The amount of work completed depends directly on the rate of work, or power. Power tells you how quickly or slowly work is being done. For example, lifting a heavy box to a high shelf requires work to move the box upward against gravity. If you lift the box slowly, it takes more time to complete the work. If you lift the box quickly, the work is done rapidly. So even though the total work may be the same, the power is greater when the work is completed in less time.

The standard unit for power is the watt. One watt is equal to one joule of work per second. So power is the rate of work or energy transfer measured in watts or joules per second.

Understanding power allows calculating important metrics like the power rating of engines, the energy efficiency of appliances, and how quickly different machines can perform work. Power also relates to important physical concepts like force and velocity. Overall, power provides crucial insight into how quickly and effectively energy can be transferred to accomplish work.

Efficiency

Efficiency is a measure of how much useful work or energy is derived from a process compared to the total energy input into that process. It provides a quantitative measure of how well a machine converts energy into useful mechanical motion.

Efficiency is calculated by dividing the useful energy or work output by the total energy input, and is usually expressed as a percentage. The higher the efficiency percentage, the more useful energy is extracted from the energy source.

For example, if a motor takes 100 Joules of electrical energy as input and converts it into 70 Joules of rotational kinetic energy, its efficiency would be:

Efficiency = (Useful energy output) / (Total energy input)
= 70 J / 100 J = 0.70

Therefore, this motor is 70% efficient. In a perfectly efficient machine, the efficiency would be 100%, however in real systems some energy is always lost or wasted as heat, sound, or friction. Improving efficiency is an important goal in engineering design to maximize the useful output for a given energy input.

Real-World Applications

Mechanical energy principles are applied in many real-world technologies and engineering systems. Here are some examples:

Vehicles: Gasoline engines, electric motors, and other power sources in cars, trucks, planes, etc. convert energy into mechanical energy to propel the vehicle. Energy concepts like power, torque, efficiency are central to vehicle design.

Electrical Power Generation: Turbines in hydroelectric dams, wind farms, etc. use mechanical energy from moving fluids to generate electricity. The design focuses on efficiently converting mechanical energy to electrical energy.

Robotics: Robots are engineered to use motors and actuators that harness mechanical energy to move the arms/wheels, grip objects, and complete tasks. Careful mechanical design is needed to enable robot movements.

Manufacturing Equipment: Factory machines like conveyor belts, presses, and assembly robots all use principles of mechanical energy and power transmission to operate efficiently, safely and with precision.

Understanding mechanical energy concepts allows engineers to properly design, build, and optimize these complex systems to function as intended.

Mechanical Energy and Other Types of Energy

Mechanical energy is very different than other common forms of energy like thermal, electric, chemical, and nuclear energy. While mechanical energy has to do with the motion and position of objects, other types of energy involve different physical phenomena.

Thermal energy comes from the kinetic energy of atoms and molecules in an object. The faster the atoms move, the higher the thermal energy. Thermal energy is related to temperature. Electric energy comes from the movement of electrons. Chemical energy is stored within the bonds between atoms in molecules. Nuclear energy comes from changes within atomic nuclei.

Unlike mechanical energy, thermal, electric, chemical, and nuclear energy involve energy stored at the atomic or molecular level. Mechanical energy deals with the physics of macroscopic objects. While mechanical energy can be converted to and from other forms, the fundamental characteristics are very distinct.

Mechanical energy is easy to observe and measure in the everyday world. A moving car contains kinetic energy. A compressed spring contains potential energy. Mechanical energy is involved any time an object moves or has position. The other energy types are less visible on a large scale and involve different scientific principles.

In summary, mechanical energy fundamentally differs from thermal, electric, chemical, and nuclear energy. Mechanical energy underlies the motion and position of tangible objects, while other energy forms operate at the atomic and molecular levels in different ways. This makes mechanical energy unique and distinct within the broader study of physics and energy.

Conclusion

The key findings about mechanical energy are that it is the energy possessed by objects due to their motion or position. Mechanical energy has two components: kinetic energy, which is energy due to an object’s motion, and potential energy, which depends on an object’s position or condition. Mechanical energy is subject to the law of conservation of energy, so the total mechanical energy in a closed system remains constant. Even as energy transforms between kinetic and potential forms, the total amount of mechanical energy is conserved. Understanding mechanical energy and how to calculate it using parameters like mass, velocity, height, and spring constant allows predicting and describing motion in physical systems. Mechanical energy plays a fundamental role across many real-world systems and technologies, from simple machines like pendulums to complex systems like rollercoasters. Mastering mechanical energy is crucial for fields like physics, engineering, and many others.