Is Kinetic Energy Converted To Potential Energy?

Kinetic energy and potential energy are two forms of mechanical energy. Kinetic energy is the energy associated with motion and potential energy is stored energy based on an object’s position or configuration. The law of conservation of energy states that the total mechanical energy in a closed system remains constant. This means that energy can change forms within a system, going from kinetic to potential or vice versa, but the total amount of energy stays the same.

Table of Contents

Kinetic Energy

Kinetic energy is the energy an object has due to its motion. The amount of kinetic energy depends on both the mass and velocity of the object. Some key things to know about kinetic energy:

The kinetic energy (KE) of an object is calculated using the formula: KE = 1/2 mv^2

Where m is the mass of the object and v is its velocity.
Since kinetic energy depends on an object’s velocity squared, the faster an object moves, the more kinetic energy it has.
Some examples of kinetic energy in action include:
- A moving car
- The motion of wind, water, or flowing liquids
- The movement of people or animals

In summary, kinetic energy arises from motion. The amount of kinetic energy present increases rapidly as the velocity increases. Understanding kinetic energy is key to understanding concepts like momentum, work, and power.

Potential Energy

Potential energy refers to energy that is stored within a system due to its position or configuration. An object’s potential energy represents the maximum amount of energy that the object is capable of releasing. Some common forms of potential energy include:

Gravitational potential energy: This is energy stored within an object due to the influence of gravity. For example, a rock held at the top of a hill contains gravitational potential energy. The amount of gravitational potential energy it has depends on its mass, its height above the ground, and the acceleration due to gravity.

Elastic potential energy: When a spring, rubber band, or other elastic object is stretched or compressed, it stores elastic potential energy. That elastic potential energy can be converted to kinetic energy if released.
Chemical potential energy: Energy stored within the bonds of atoms and molecules is called chemical potential energy. This energy can be released when chemical bonds are broken through chemical reactions. Examples include fossil fuels, batteries, food, and explosives.

Potential energy is important because it allows energy to be stored and moved from one place to another. The potential energy stored within an object or system can easily be converted to kinetic energy. This potential to kinetic energy conversion is what allows many machines and systems to operate.

Relationship Between Kinetic and Potential Energy

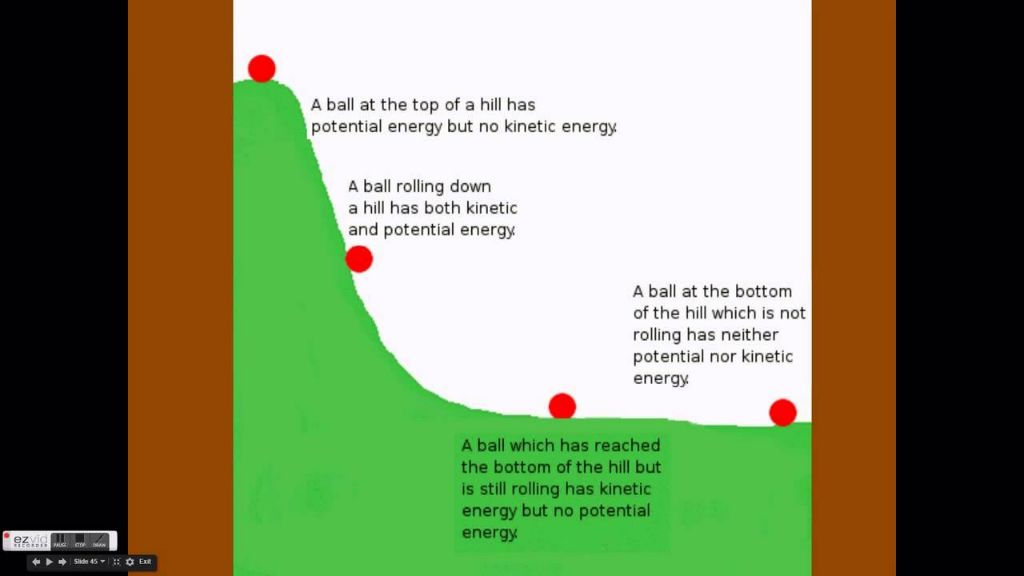
Kinetic and potential energy share an interconnected relationship and can transform between each other during the motion of an object or system. As an object or system gains kinetic energy through motion, it loses potential energy and vice versa.

For example, when an object falls due to gravity, it loses potential energy and gains an equal amount of kinetic energy as it accelerates. When the object then hits the ground, its kinetic energy is absorbed or transferred until the object slows to a stop. During this slowdown, the object loses kinetic energy but does not gain any potential energy.

This exchange of kinetic and potential energy works can also work in the opposite direction. If a spring is stretched or compressed, it gains potential energy that can be converted into kinetic energy when released, launching the attached object or system upwards until it depletes the gained potential energy. At the peak height, all potential energy has been converted to kinetic energy until gravity slows the upward motion, draining kinetic energy and redirecting the cycle.

Conservation of Mechanical Energy

The principle of conservation of mechanical energy states that in a closed system without any nonconservative forces, the total mechanical energy remains constant. Mechanical energy refers to the sum of an object’s kinetic energy and potential energy.

This means that energy can be converted back and forth between kinetic and potential energy, but the total amount of mechanical energy stays the same. For example, when a ball rolls down a hill, it loses potential energy but gains kinetic energy. The amount gained in kinetic energy is equal to the amount lost in potential energy, so the total mechanical energy is conserved.

The conservation of mechanical energy is an application of the more general law of conservation of energy. It applies specifically to mechanical systems where only conservative forces like gravity and springs are involved. As long as no energy is lost to thermal energy or other dissipative forces, mechanical energy will be conserved.

This principle allows us to analyze mechanical systems without having to consider energy losses. We can track the transformations between potential and kinetic energy during motions while knowing that the total amount of mechanical energy in the system stays constant.

Examples of Energy Conversion

Kinetic and potential energy conversion happens all around us. Here are some everyday examples:

Pendulums: As a pendulum swings, the bob continuously converts kinetic energy to gravitational potential energy and back again in a cyclic motion.
Roller coasters: At the top of a hill on a roller coaster track, the car has maximum gravitational potential energy. As it travels downhill it accelerates due to gravity, converting that potential energy into kinetic energy.

Springs: When a spring is compressed or stretched away from its relaxed state, it stores elastic potential energy. When released, the spring converts that energy into kinetic energy.

In all these examples, energy is transferred back and forth between potential and kinetic, while the total mechanical energy remains constant (assuming no nonconservative losses).

Nonconservative Forces

While in ideal conditions, the law of Conservation of Mechanical Energy means that the total mechanical energy of a closed system remains constant, there are some situations where the law does not hold true. Forces that result in mechanical energy not being conserved are known as nonconservative forces. The most common example of this is friction.

When an object moves against a frictional force, some of its mechanical energy gets converted to thermal energy in the form of heat. For example, when a ball rolls across the ground, friction between the ball and the ground results in mechanical energy from the motion of the ball to be converted into thermal energy. This leads to the ball slowing down and heating up due to friction. The mechanical energy is not conserved – some of it is transformed to heat energy instead.

Therefore, while the total energy including thermal energy may be conserved in principle, the mechanical energy is reduced. Friction converts kinetic and potential energy to thermal energy, rather than potential energy. This is why the law of Conservation of Mechanical Energy fails to apply – the mechanical energy gets dissipated as thermal energy due to nonconservative forces like friction acting on the system.

Limits to Conservation

Strictly speaking, conservation of energy does not hold at the atomic scale. According to quantum mechanics, energy can be “borrowed” from empty space as long as it is paid back quickly enough that the accounting discrepancies cannot be detected at the macroscopic level. These quantum fluctuations allow transitions between atomic energy levels that would otherwise violate conservation of energy. However, over long enough timescales that account for a large enough number of particles, these discrepancies average out so that the total energy of macroscopic systems is still observed to be conserved.

Summary

Kinetic energy and potential energy are forms of mechanical energy. Kinetic energy is the energy of motion – an object with more speed has more kinetic energy. Potential energy is stored energy due to an object’s position or shape – an object at a higher altitude or an object that is compressed or stretched has more potential energy.

The law of conservation of mechanical energy states that in an isolated system without nonconservative forces, the total mechanical energy remains constant. This means that kinetic and potential energy can be converted back and forth between each other, while the total amount of mechanical energy stays the same.

For example, when a ball falls, its potential energy is converted into kinetic energy. As it bounces back up, its kinetic energy is converted back into potential energy. Friction and air resistance are examples of nonconservative forces that can remove mechanical energy from a system over time.

In summary, kinetic energy and potential energy can interchange between each other, demonstrating the conversation of mechanical energy. However, nonconservative forces can limit this conservation over time.

Conclusion

In summary, kinetic energy and potential energy can convert between one another under certain conditions and within limits. Within a closed system where only conservative forces like gravity act, mechanical energy (kinetic + potential) is conserved according to the law of conservation of energy. Kinetic energy can convert into potential energy in cases like a roller coaster going up a hill. The kinetic energy is transferred into gravitational potential energy. Then that gravitational potential energy can be converted back into kinetic energy as the roller coaster goes downhill.

While energy conversion between kinetic and potential happens readily in idealized systems, in the real world there are often frictional forces or air resistance that can change, dissipate, or remove mechanical energy from the system. So perfect conservation does not always apply. Additionally, energy conversions only work cleanly when conservative versus nonconservative forces are properly accounted for.

But when analyzing basic physics problems dealing with gravity, springs, pendulums and other elastic objects, ramps, etc. that kinetic and potential energy interconversion serves as a handy model. Just be sure to double check the assumptions and parameters to ensure kinetic and potential energy should theoretically be conserved as energy transfers between the two forms.