How Do You Solve For Kinetic And Potential Energy?
Kinetic energy is the energy an object has due to its motion. The faster an object moves, the more kinetic energy it has. Kinetic energy can be transferred between objects during collisions. Potential energy is stored energy an object has due to its position or shape. There are several types of potential energy including gravitational potential energy, elastic potential energy, and chemical potential energy.
The key difference between kinetic and potential energy is that kinetic energy depends on motion while potential energy depends on an object’s position or structure. Kinetic energy changes as an object speeds up or slows down. Potential energy changes as an object moves to different positions in a field of force or as its structure changes. Understanding the difference between kinetic and potential energy is crucial when solving mechanical energy problems.
Kinetic Energy Formula
The formula for kinetic energy is:
KE = 1/2 x m x v2
Where:
- KE is the kinetic energy in joules (J)
- m is the mass of the object in kilograms (kg)
- v is the velocity of the object in meters per second (m/s)
This formula shows that kinetic energy depends on two variables – the mass of the object and the square of its velocity. The heavier the object and the faster it is moving, the more kinetic energy it possesses. The 1/2 multiplier is needed to calculate the proper value for kinetic energy based on the units being used.
Potential Energy Formula
The formula for potential energy is:
PE = mgh
Where:
- PE is the potential energy, measured in joules (J)
- m is the mass of the object, measured in kilograms (kg)
- g is the acceleration due to gravity, which is 9.8 m/s2 on Earth
- h is the height of the object, measured in meters (m)
Breaking this down:
- Mass (m) represents the amount of matter in an object.
- Gravity (g) produces a downward force on objects proportional to their mass.
- Height (h) is the vertical position of the object relative to a reference point.
- Together, the mgh factors represent the amount of potential energy possessed by an object at a given height.
So in summary, the potential energy formula shows that the potential energy of an object depends on its mass, gravity, and height.
Examples of Kinetic Energy
Kinetic energy is energy associated with motion. Some common examples of kinetic energy in everyday life include:
- A moving car, truck, bus, or other vehicle
- A soccer ball being kicked
- A flying airplane
- A flowing river or stream
- The wind blowing
- A roller coaster going down a hill
- A skateboarder rolling down a ramp
- A bowling ball rolling down a lane
- A person running, walking, swimming, biking, etc.
- Molecules and atoms moving and vibrating
In all these examples, and many more, the objects in motion have kinetic energy. The faster the object moves, the more kinetic energy it possesses. Kinetic energy depends on both the mass and velocity of an object. Understanding kinetic energy helps explain the workings of the physical world.
Examples of Potential Energy
Potential energy is the stored energy in an object due to its position or state. Here are some common real-world examples of potential energy:
Gravitational Potential Energy
When you lift an object upwards, you are moving it against the downward pull of gravity. This gives the object gravitational potential energy equal to the weight of the object multiplied by the height it is lifted. For example, lifting a 5kg book from the floor onto a 2m high shelf gives the book 9.8 x 2 = 19.6 Joules of gravitational potential energy.
Elastic Potential Energy
Stretching or compressing springs and elastic bands stores elastic potential energy in them. The energy is stored due to the deformation of the elastic material. For example, stretching a spring a certain distance requires force to overcome the spring’s restorative force. When released, the spring converts the stored elastic potential energy into kinetic energy.
Chemical Potential Energy
Energy stored in the chemical bonds of substances like fuels, foods, batteries and explosives is called chemical potential energy. This energy gets released when chemical bonds are broken via reactions like burning, digestion, or explosions. For example, the chemical energy stored in a car’s gasoline is converted into kinetic energy to move the car.
Converting Between Kinetic and Potential Energy
Kinetic and potential energy can convert back and forth between each other. This happens because energy is always conserved – it cannot be created or destroyed. Understanding how to convert between kinetic and potential energy is key for solving many physics problems.
Potential energy can become kinetic energy when the object with potential energy is allowed to move. A common example is lifting an object up to a height to give it gravitational potential energy, then letting it fall. As the object falls, the potential energy gets converted into kinetic energy from the object’s increasing velocity. The total amount of energy remains constant, just changing form.
Kinetic energy can convert into potential energy when an object’s motion is impeded. For example, a ball has kinetic energy when rolling, but slows to a stop as it rolls up a slope. The ball’s kinetic energy has gone into gravitational potential energy from being lifted up the slope. The energy again stays constant, just shifting from kinetic to potential form.
Understanding these conversions allows us to apply conservation of energy when solving physics problems. We can set the initial total mechanical energy equal to the final total mechanical energy, knowing that energy is never lost but only changes form. This is a key concept for analyzing many motion and collision scenarios.
Solving Problems with Kinetic Energy
To solve problems using the kinetic energy formula, you first need to identify the values provided in the problem and determine which variable you need to solve for. The kinetic energy formula is:
Ek = 1/2 mv2
Where m is the mass of the object in kg, and v is the velocity of the object in m/s. Let’s look at some examples:
Example 1: A car with a mass of 1200 kg is traveling at 20 m/s. What is its kinetic energy?
To solve:
m = 1200 kg
v = 20 m/s
Ek = 1/2 x 1200 x (20)2
= 1/2 x 1200 x 400
= 240,000 J
Example 2: A baseball with a mass of 0.15 kg is hit with a velocity of 35 m/s. What is its kinetic energy?
To solve:
m = 0.15 kg
v = 35 m/s
Ek = 1/2 x 0.15 x (35)2
= 1/2 x 0.15 x 1225
= 91.875 J
So in summary, when solving kinetic energy problems:
– Identify the values for mass and velocity
– Plug them into the formula Ek = 1/2 mv2
– Solve for the kinetic energy
Solving Problems with Potential Energy
The potential energy formula allows us to calculate the potential energy stored in an object based on its mass, height, and the force of gravity. Here are some examples of using the potential energy formula to solve problems:
A 5kg book is sitting on a shelf 2 meters above the ground. To find the potential energy of the book, we use the formula:
PE = mgh
Where m is mass (5 kg), g is gravity (9.8 m/s2), and h is height (2 m). Plugging this in:
PE = (5 kg)(9.8 m/s2)(2 m) = 98 J
So the potential energy of the book on the shelf is 98 J.
As another example, let’s say a 12kg bicycle is lifted up a hill that has an incline of 30 degrees and a vertical height of 5m. To find the potential energy, we would use the same formula, but adjust the height to account for the incline. The vertical component of the incline is:
Vertical height = (5 m)sin(30 degrees) = 2.5 m
Then plugging into the formula:
PE = (12 kg)(9.8 m/s2)(2.5 m) = 294 J
So the potential energy of the bicycle lifted up the inclined hill is 294 J. This shows how the potential energy formula can be applied to calculate the stored energy of objects based on their mass, height, and gravity. Problems can involve adjusting the height for inclines or accounting for changes in gravity. With the formula, we can solve for the potential energy in various practical situations.
Conservation of Mechanical Energy
The law of conservation of mechanical energy states that in a closed system without any external forces, the total mechanical energy remains constant. Mechanical energy is the sum of an object’s kinetic and potential energies. This means that the amount of kinetic and potential energy within a system may change, but the total amount of mechanical energy stays the same. Energy is never created or destroyed, just converted between different forms.
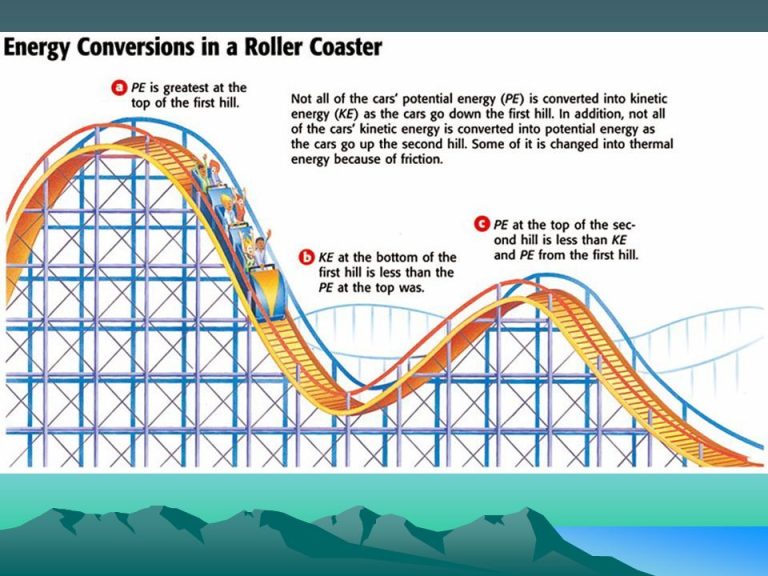
For example, consider a ball rolling down a ramp. At the top of the ramp, the ball has a high amount of potential energy and no kinetic energy. As it rolls down, it loses gravitational potential energy but gains kinetic energy. The amount of potential energy lost equals the amount of kinetic energy gained. The mechanical energy at the bottom equals the mechanical energy at the top – energy is conserved. Another example is a pendulum swinging back and forth. At the endpoints of the swing, it has maximum potential energy. At the lowest point, it has maximum kinetic energy. The transfer between potential and kinetic energy conserves the total mechanical energy.
Understanding conservation of mechanical energy is useful for analyzing mechanical systems and solving physics problems. It allows you to equate the initial and final mechanical energies to find unknown values. Many real-world systems like roller coasters, springs, and pendulums follow this important law of physics.
Common Misconceptions
There are a few common misconceptions when it comes to kinetic and potential energy:
One is thinking that potential energy is not “real” energy. This is incorrect – potential energy very much exists and is part of the total mechanical energy of a system. An object at rest still contains energy in the form of potential energy.
Another misconception is believing kinetic energy depends on velocity rather than velocity squared. The kinetic energy formula shows that kinetic energy is directly proportional to the mass and the square of the velocity. Doubling the velocity does not double the kinetic energy, but rather quadruples it.
Additionally, some believe that as an object falls, its potential energy is converted directly into kinetic energy. This is not quite right – some of the potential energy goes into work against air resistance and friction during the fall. The sum of kinetic and potential energy is conserved, but they do not directly convert between one another.
Finally, there is sometimes confusion about whether kinetic or potential energy is “better” or more useful. However, they are both important forms of mechanical energy and it depends on the situation whether kinetic or potential energy is more useful.