What Is Work As It Relates To Energy?

Definition of Work

In physics, work is defined as the amount of force applied over a certain distance. Specifically, work W is equal to the dot product of force F and displacement d. This relationship can be expressed mathematically as:

W = F • d

Where F is the force vector and d is the displacement vector. Force and displacement must be in the same direction for positive work to be done. If force and displacement are perpendicular, the work is zero. If they are anti-parallel, work is negative.

Work is a transfer of energy. When positive work is done, energy is transferred to an object and increases its energy. Negative work means energy is removed. The units of work are typically joules (J) or newton-meters (N*m).

In summary, work in physics is defined as force multiplied times distance. This is the basis for concepts like the work-energy theorem, power, and mechanical advantage. Work is a way of quantifying energy transfers in mechanical systems.

Work and Energy

Work and energy are closely related concepts in physics. When a force acts on an object and causes it to move, work is said to be done on the object. The work done on the object transfers energy to the object.

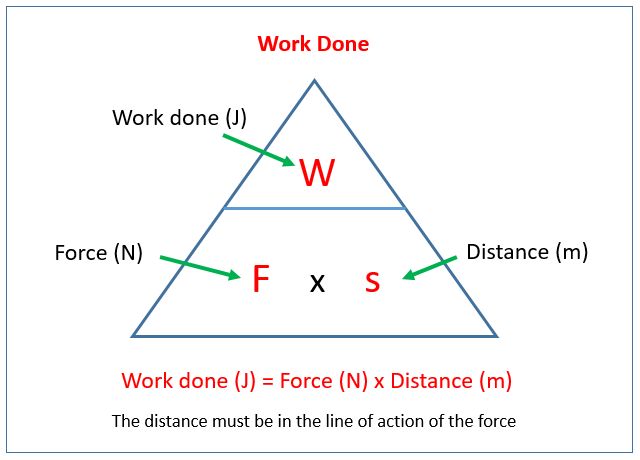
The amount of work done is equal to the magnitude of the force (F) times the distance (d) moved by the object in the direction of the force. This relationship is described by the equation:

Work = Force x Distance
W = Fd

So if a 10 Newton force acts on an object and moves it 3 meters in the direction of the force, the work done would be:

Work = Force x Distance
= 10 N x 3 m
= 30 Nm (Newton-meters)

The unit for work is the Newton-meter (Nm) or Joule (J). The amount of work done on an object equals the amount of energy transferred to the object. This energy enables the object to do things like move, lift objects, or increase temperature. The work-energy theorem states that the net work done on an object is equal to its change in kinetic energy. This shows the direct relationship between work and energy.

Units of Work

When an object is moved by a force, work is done on the object. More specifically, work is defined as force applied over a distance. Since work involves producing movement, it is measured in units of energy.

The standard SI unit of measurement for work is the joule (J). One joule is defined as the work done by a force of one newton when it moves an object one meter. The joule is also the SI unit for all forms of energy.

Other common units used to measure work include:

• Kilojoule (kJ) = 1,000 joules
• Megajoule (MJ) = 1,000,000 joules
• Gigajoule (GJ) = 1,000,000,000 joules
• Calorie (cal) = 4.184 joules
• Kilocalorie (Cal or kcal) = 4,184 joules
• British thermal unit (BTU) = 1,055 joules
• Foot-pound (ft-lb) = 1.356 joules

When calculating work, it’s important to pay attention to units to ensure accurate results. The joule allows quantitative analysis of work and energy across scientific fields.

Work-Energy Theorem

The work-energy theorem states that the net work done on an object equals its change in kinetic energy. This is represented by the mathematical equation:

W_net = ΔK

Where:

• W_net is the net work done on the object
• ΔK is the change in kinetic energy of the object

This theorem shows that work done on an object transfers energy to the object, increasing its kinetic energy. Some key points about the work-energy theorem:

• The net work accounts for all forces acting on the object, including non-conservative forces.
• The kinetic energy depends on the mass and velocity of the object.
• Work and kinetic energy are measured in the same units (joules in the SI system).
• The theorem can be used to solve problems involving work, kinetic energy, and motion.

The work-energy theorem is a fundamental relationship in classical physics and has broad applications in mechanical systems and engineering.

Power

Power is defined as the rate at which work is done. It refers to how quickly or slowly work is performed. Power is measured in watts (W), where 1 watt is equal to 1 joule of work performed per second.

For example, a lightbulb that uses 100 watts of power performs 100 joules of work every second by converting electrical energy into light and heat energy. The more power something uses, the faster it can perform work. Power can also refer to the rate at which energy is transferred or converted from one form to another.

Some common equations involving power are:

• Power (P) = Work (W) / Time (t)
• Power = Force (F) x Velocity (v)
• Power = Voltage (V) x Current (I)

Power measures the speed of doing work or the speed of energy transfer. High power systems or devices can perform work rapidly, while low power systems are slower. Understanding power usage and transfer rates is important in many fields of science and engineering.

Mechanical Advantage

Mechanical advantage is defined as the ratio of output force to input force for any simple machine or mechanical device. It refers to the multiplication of force that occurs when a machine converts the input force applied into output force. The mechanical advantage enables a smaller input force to overcome a larger output force more easily.

The mechanical advantage can be calculated as:

Mechanical Advantage = Output Force / Input Force

For example, a lever amplifies an input force by distributing it over a greater output distance. The mechanical advantage of a lever depends on the relative lengths of the input and output arms. A longer output arm results in greater mechanical advantage as it allows a smaller input force to overcome a larger output force.

Other simple machines like pulleys, gears, inclined planes, and screws also provide mechanical advantage in different ways to reduce the magnitude of forces needed to accomplish work. The tradeoff is that the machine moves the output load over a longer distance than the input force.

Understanding mechanical advantage helps optimize the design of machines and mechanisms to maximize efficiency. It enables accomplishing tasks that would otherwise require impractically large input forces without the machine.

Efficiency

Efficiency measures the ratio of useful output energy or work to the total input energy or work in a system. It quantifies how well the system converts input energy into desired output energy. Efficiency is commonly expressed as a percentage:

Efficiency = (Useful output energy or work) / (Total input energy)

For example, if a motor requires 100 Joules of electrical energy as input but produces only 80 Joules of mechanical work as output, its efficiency would be:

Efficiency = 80 J / 100 J = 80%

The remaining 20 Joules was likely lost or wasted as heat, sound, or friction within the motor. The higher the efficiency percentage, the more useful output is generated per unit of input. Improving efficiency reduces energy waste and costs.

Engineers often aim to maximize efficiency in energy conversion systems like motors, generators, appliances, vehicles, and power plants. More efficient systems require less input energy to achieve a given output. This saves on fuel, electricity, or other resources.

However, there are always some conversion losses and tradeoffs. 100% efficiency is ideal but not realistically achievable. Some loss of usable energy is inevitable in real-world systems.

Forms of Energy

Energy comes in different forms that can be categorized into two main types – potential energy and kinetic energy. Potential energy is stored energy that has the potential to do work, while kinetic energy is energy in motion. The different forms of energy include:

Potential Energy

Potential energy can be stored in objects by virtue of their position or state. Forms of potential energy include:

• Gravitational Potential Energy – The energy stored in an object due to its height in a gravitational field.
• Elastic Potential Energy – The energy stored in elastic objects that are deformed.
• Chemical Potential Energy – The energy stored in the chemical bonds of substances.
• Nuclear Potential Energy – The energy stored in the nucleus of an atom.

Kinetic Energy

Kinetic energy is the energy of motion and exists in various forms:

• Mechanical Energy – The sum of an object’s kinetic and potential energy.
• Radiant Energy – Energy carried by electromagnetic radiation such as light.
• Thermal Energy – The total kinetic energy of molecules in a substance.
• Sound Energy – Energy carried by sound waves.
• Electrical Energy – Energy from the movement of charged particles.

Understanding the different forms of energy is essential when studying thermodynamics and doing work involving energy transfers and transformations.

Conservation of Energy

One of the most fundamental principles in physics is the law of conservation of energy. This states that the total amount of energy in an isolated system remains constant over time. Energy cannot be created or destroyed, only converted from one form into another.

For example, when a book falls off a table, the potential energy due to its height gets converted into kinetic energy as it accelerates towards the ground. When the book hits the floor, the kinetic energy gets converted into sound, heat, and deformation energy. While the forms of energy change, the total amount of energy within the closed system (the book and the Earth) remains the same.

This conservation law applies to all isolated systems, from chemical reactions to even the entire universe. It is why perpetual motion machines are impossible – there is always some energy loss in any process. The law of conservation of energy is a cornerstone of physics and helps describe many processes in nature and technology.

Real World Examples

The principles governing work and energy have many practical applications in the real world.

In machinery and engineering, work concepts are critical for understanding how devices like motors, engines, and generators operate. For example, the amount of useful work an engine can perform is limited by its thermal efficiency – the percentage of heat energy that is converted into mechanical work. Improving efficiency allows more work to be extracted from a given fuel source.

In biology, muscles perform mechanical work on the body by converting chemical energy from food into kinetic energy. The rate at which work is done corresponds to power output. Athletes can increase their power and overall fitness through training that builds muscle strength and endurance.

Thermodynamics applies work concepts to systems and processes that involve heat transfer and energy transformations, like those found in steam engines and refrigerators. The first and second laws of thermodynamics use work and heat to characterize the limits of how efficiently such systems can operate.

Understanding the work-energy relationship helps engineers optimize designs to maximize performance, athletes structure their training, and scientists analyze processes that would otherwise seem mysterious. The foundational principles at play underscore much of the mechanical world around us.