What Is The Relation Between Gravitational Potential Energy And Potential?
Definition of Gravitational Potential Energy
Gravitational potential energy is the energy stored in an object due to its position within a gravitational field. Gravity provides the force to do work on an object that is moved in the gravitational field, which gives that object gravitational potential energy.
The gravitational potential energy of an object depends directly on three factors:
- The object’s mass – more massive objects have more gravitational potential energy
- The object’s height above a reference position – the higher it is, the more potential energy it has
- The strength of the gravitational field – stronger fields provide more potential energy
Gravitational potential energy can be converted to kinetic energy if the object falls through the gravitational field. The object’s potential energy will be converted to kinetic energy as gravity accelerates it. This demonstrates the conservation of mechanical energy in classical physics.
Definition of Potential
Potential is a scalar quantity representing the potential energy per unit mass at a position in a conservative field. It is measured in joules per kilogram (J/kg).
Potential can be thought of as the amount of potential energy possessed by a unit mass at a particular location. For example, gravitational potential describes the gravitational potential energy per unit mass in a gravitational field, which depends on the distance from the source of gravity. The gravitational potential is always negative and approaches zero as the distance from the gravitating body increases. Similarly, electric potential represents the electric potential energy per unit charge at a point in an electric field. It is typically measured in volts. The electric potential increases as you move closer to a positive charge and decreases as you move away.
Potential energy is stored energy associated with the configuration of a system in a conservative field. The potential represents that potential energy normalized per unit mass or charge. It is useful for calculating the potential energy for any mass or charge based on its position in the field. Potential provides a convenient way to characterize the potential energy available in a system.
Relation Between the Two
Gravitational potential energy at a point equals mass times gravitational potential at that point. Gravitational potential quantifies the potential energy per unit mass. Conceptually, gravitational potential refers to the work done per unit mass in moving an object in a gravitational field from a reference location to a specified point. Gravitational potential energy then depends on the object’s mass and the gravitational potential at that location.
Gravitational potential, denoted as V, mathematically equals the negative of the work done by the gravitational force, per unit mass, in moving an object from the reference location to that point. The equation is:
V = -W/m
Where W is the work done by gravity and m is the object’s mass. The gravitational potential energy of an object of mass m at that point is therefore:
U = mV
Where U is the gravitational potential energy. So in summary, gravitational potential energy is directly proportional to both the object’s mass and the gravitational potential at that location.
Calculating Gravitational Potential
Gravitational potential is calculated as the gravitational potential energy of an object divided by its mass. It represents the amount of potential energy per unit mass at a given position in a gravitational field. The gravitational potential only depends on the position of the object in the field, not the path it took to get there.
Mathematically, gravitational potential is calculated using the following equation:
Gravitational Potential = Gravitational Potential Energy / Mass
Where:
- Gravitational Potential Energy = mass x gravity x height above reference point
- Mass = mass of the object
- Gravity = gravitational field strength (9.8 m/s2 on Earth)
Gravitational potential does not depend on the path taken by the object to reach its position. This is because gravitational potential energy is a state function and only depends on the object’s height, not how it got there.
As a result, gravitational potential at a given point in space is the same no matter what path an object took to get there. This allows gravitational potential to be mapped as a scalar field independent of trajectory.
Examples and Applications
Gravitational potential energy has many practical real-world examples that demonstrate the relation between potential energy and gravitational force. Here are some common examples:
Rolling balls down ramps, swinging pendulums, launching projectiles
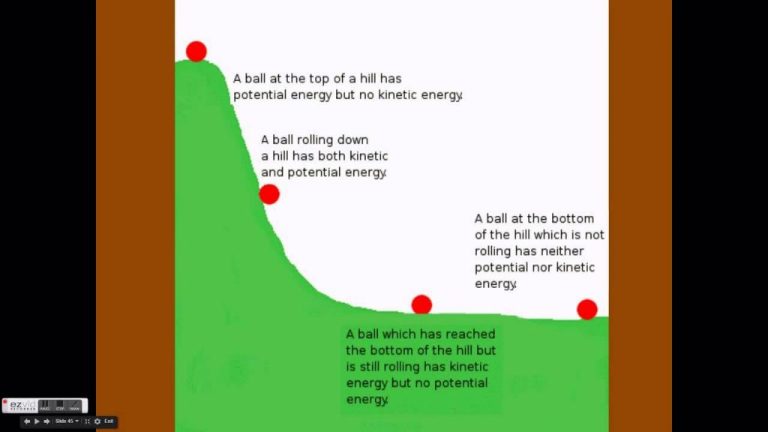
A classic physics experiment is rolling a ball down a ramp to observe the conversion between potential energy at the top of the ramp into kinetic energy as the ball rolls down. The ball gains speed as it drops in height, showing the direct correlation between potential energy stored and kinetic energy gained.

Pendulums work on the same principle, with the bob gaining potential energy at the top of the swing’s arc. As it swings down, this potential energy converts into kinetic energy and speed. Projectiles like balls, arrows, or bullets shot upwards also demonstrate potential becoming kinetic, stopping at their maximum height as the energy converts fully to potential.
Satellite orbits, tides, planet and star formations
The gravity between celestial bodies like satellites, planets, stars, and galaxies shows gravitational potential energy in space. Satellites maintain orbital periods and velocities in relation to the large gravitational potentials between them and planets.
The Moon’s gravity causes tidal bulges on Earth due to gravitational potential differences from the near and far sides of Earth. Gravitational collapse formed planets, stars, and galaxies as material was drawn together by growing gravitational potential.
Conservation of Mechanical Energy
Total mechanical energy, which is the sum of kinetic energy (KE) and potential energy (PE), is conserved in closed systems. This means the total amount of mechanical energy remains constant, even as energy transforms between potential and kinetic forms.
Gravitational potential energy can readily convert into kinetic energy and vice versa in closed systems. For example, as a ball falls, its potential energy decreases while its kinetic energy increases. However, the total mechanical energy (PE + KE) remains the same. This illustrates the conservation of mechanical energy due to the gravitational force.
Differences from Electric Potential
Gravitational potential energy is quite distinct from electric potential energy, despite some apparent similarities. Here are some of the key differences:
Electric potential depends on the electric charge of a particle, whereas gravitational potential depends on the mass of an object. Charges can be positive or negative, but mass is always positive. So the physics governing gravitational and electric potentials have important distinctions.
Additionally, electric potential obeys the principle of superposition. This means that the total electric potential at any point is simply the sum of potentials due to each charge. However, gravitational potentials do not superimpose in this way. The gravitational force between two masses is not a simple sum of their individual potentials.
These differences stem from the fact that electric forces involve positive and negative charges, while gravity only involves positive mass. The different nature of the fundamental forces leads to different mathematical behaviors for electric and gravitational potentials.
Applications in Physics
Understanding how gravitational potential energy relates to potential has
important applications in physics. One of the main areas where the relationship is utilized
is in analyzing and predicting orbits and trajectories.
The gravitational potential at any point in a gravitational field determines the kinetic energy and velocity an object will have at that point. This allows physicists to model how objects like satellites and planets will move through space.
As an object moves in a gravitational field, it exchanges gravitational potential energy for kinetic energy and vice versa. Calculating the gravitational potential energy based on the object’s height in the field shows how much kinetic energy it will gain or lose. This is key to modeling gravity and orbital mechanics.
Overall, the connection between gravitational potential energy and potential provides physicists with the quantitative tools to describe motion under gravity. It underlies our modern understanding of astronomy, space flight, and many other important physics applications.
Importance and Significance
The relationship between gravitational potential energy and potential is of crucial importance in physics and our understanding of the universe. This concept has served as a fundamental building block of modern physics and astronomy for centuries.
Gravitational potential and the associated potential energy are key to explaining gravitational forces and the motion of objects through space. Isaac Newton’s law of universal gravitation first quantified the relation between mass, distance, and gravitational force. The gravitational potential function came out of classical mechanics and provided a mathematical framework to calculate the potential energy of an object based on its mass and position in a gravitational field.
This breakthrough enabled physicists to mathematically model gravitational systems like planetary orbits. It also laid the foundation for critical concepts like conservation of energy and mechanical work. The gravitational potential function and energy continue to play central roles in modern physics today.
Understanding gravitational potential has allowed humans to launch satellites, travel to the Moon, and gain insights into the evolution of stars, galaxies, and the cosmos itself. This essential concept underlies our comprehension of many astrophysical phenomena. Derivations of gravitational potential energy also have important implications for fields like quantum mechanics.
By elucidating the relationship between gravitational potential and energy, physicists have shaped our fundamental grasp of the forces that govern motion across the universe. Their enduring importance cannot be overstated.
Current Research
Gravitational physics continues to be an active area of research and scientific advancement. Some key areas of current research related to gravitational potential energy include:
Refinement of gravitational physics and expanding universe models: As experiments and observations push the boundaries of physics, theories like general relativity are being refined and expanded. This includes research into gravity waves, refinements to the Standard Model of cosmology, and investigations into dark matter and dark energy.
Exploring extremes like black holes, neutron stars, and singularities: Compact stellar objects like black holes allow researchers to study gravitational forces and potentials at their extremes. Important recent discoveries include the first image of a black hole and better understandings of black hole collisions.
Unification efforts: Many physicists are working towards a unified theory that brings together gravity and quantum mechanics. Learning more about gravitational potential energy may bring us closer to a Theory of Everything.
Astrophysics and cosmology: Understanding gravitational potential energy remains crucial to mapping galactic motion, modeling the evolution of the universe, and studying dark matter halos around galaxies.
Applying gravitation concepts to new areas: Researchers are finding new applications for gravitational principles in diverse fields like developing gravity batteries and energy harvesting approaches leveraging gravitational potential.