What Is The Equation For Hydropower In Imperial Units?
Hydropower, also known as hydroelectric power, is a renewable energy source that generates electricity by using the energy from flowing water. Hydropower plants capture the energy of falling or fast-moving water to spin turbines that are connected to generators (https://www.hydropower.org/iha/discover-facts-about-hydropower). The spinning generators produce electricity that can be transmitted and distributed for residential, commercial and industrial uses.
In the imperial system of units, measurements are in feet, gallons, pounds, etc. as opposed to the metric system which uses meters, liters, kilograms, etc. The imperial system is commonly used in the United States.
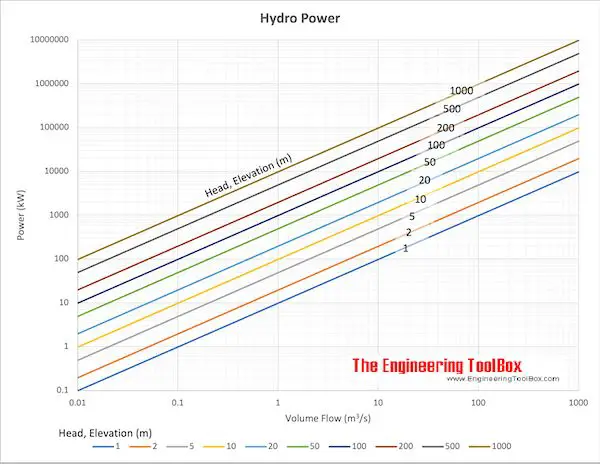
The amount of power generated by a hydropower system can be calculated using the hydropower equation. This equation takes into account the head (vertical distance the water falls), flow rate (volume of water per second), efficiency (energy conversion efficiency of the turbine/generator system), and load factor (ratio of average load to peak load). The variables in the hydropower equation determine how much electricity a hydro system can produce.
Potential Energy
Potential energy is the stored energy an object has due to its position or state. In the case of hydropower, the potential energy comes from the dammed water held at an elevated height. The higher and more massive the water, the greater its potential energy. According to the study source, “The energy we get from water depends on its height or head. The head is the vertical height from the surface of the water upstream to the water’s outflow point downstream.” The gravitational force acts on the dammed water to give it this potential energy that can do work.
The potential energy (PE) of the water can be calculated using the imperial system formula:
PE = weight x height
Where:
- PE is in British thermal units (Btu)
- Weight is in pounds (lb)
- Height is in feet (ft)
So for example, 1,000 lb of water elevated 20 ft would have a potential energy of 20,000 Btu that can be harnessed to generate power.
Head
Head is defined as the vertical distance between the intake of water into the turbine and the level of discharge after the turbine. It represents the mechanical energy available to produce electricity due to the position of water.
Head (H) is typically measured in feet or inches in imperial units. It can be calculated as the difference in elevation between the water intake and discharge points:
H = Elevation at intake – Elevation at discharge
For example, if the water intake point is at 300 feet elevation, and the discharge point after the turbine is at 200 feet elevation, then the head would be:
H = 300ft – 200ft = 100ft
The greater the head or vertical drop, the more potential energy is available to be converted into electricity by the turbine generator. Head is a key factor, along with flow rate, in determining the power output capacity of a hydropower system.
Flow Rate
Flow rate, represented by Q in hydroelectric equations, refers to the volume of water that passes through the hydro facility per unit of time. It is typically measured in cubic feet per second (cfs) in imperial units. Flow rate is a key factor in determining the amount of power that can be generated by a hydro system.
To measure flow rate, the cross-sectional area of the water flow and the velocity of the water need to be determined. The cross-sectional area can be found by measuring the width and depth of the water flow channel. The velocity is trickier to measure directly, but can be calculated by using a flow meter device or by releasing a float and timing how long it takes to travel a set distance.
Once area and velocity are known, they can be multiplied together to calculate the flow rate in cubic feet per second (cfs). For example, if the channel is 5 ft wide by 2 ft deep, the area is 10 sq ft. If the float takes 5 seconds to travel 20 ft, the velocity is 4 ft/sec. Multiplying 10 sq ft by 4 ft/sec gives a flow rate of 40 cfs [1].
Efficiency
The efficiency of a hydropower system refers to the amount of potential energy that can be converted into electricity. It is expressed as a percentage and accounts for losses due to friction and turbulence as the water moves through the system.1
Typical hydropower system efficiencies range from 70% to 90%. Efficiency is mainly affected by the design of the turbine and generator. More modern turbine designs can achieve efficiencies of 90% or higher. Older systems with outdated components may have efficiencies around 70-75%. Proper maintenance and upgrades to system components can help improve efficiency over time.2
Other factors like the volume of water flow and height of the water drop (head) also impact overall efficiency. Generally, systems with higher head heights and water volumes tend to have higher efficiencies. Dams with reservoirs also allow more potential energy to be captured versus run-of-river systems.
Power
Power (P) is the rate at which energy is converted and is measured in watts (W). For hydropower, power is calculated using the potential energy of the water and the flow rate:
P = ηρgQH
Where:
- η is the efficiency of the turbine
- ρ is the density of water (62.4 lb/ft3)
- g is the gravitational acceleration (32.2 ft/s2)
- Q is the flow rate (ft3/s)
- H is the effective head (ft)
To calculate power in imperial units, the equation becomes:
P (hp) = (ηρgQH)/550
Where 550 is the conversion factor between ft-lb/s and horsepower. So power depends on both the potential energy (head and flow rate) as well as the efficiency of converting that energy into electricity.
Load Factor
The load factor is an important consideration when determining the actual power output of a hydropower system. It is defined as the ratio of the average load to the rated capacity of the system over a period of time.
Load factor accounts for the fact that hydropower systems rarely operate at full capacity all the time. The flow rate of the water source and electricity demand fluctuates throughout the day and seasonally. As a result, the average load is lower than the rated maximum capacity.
Typical load factor ranges are:
- Base load plants: 0.5 – 0.9
- Peak load plants: 0.2 – 0.5
- Pumped storage plants: 0.2 – 0.3
The load factor directly affects the utilization of the system and its financial viability. A higher load factor means the system is being used more efficiently to generate electricity.
Capacity Factor
The capacity factor is defined as the ratio of the actual energy output of a hydropower plant over a period of time compared to its potential output if it were possible for it to operate at full nameplate capacity continuously over the same time period.
According to the 2019 Hydropower Market Report by the U.S. Department of Energy, the capacity factor for hydropower plants in the United States has ranged between 35% and 45% from 2005 to 2018 [1]. This is because hydropower output depends on the available water flow, which varies seasonally and annually. The capacity factor represents the average expected energy production divided by the energy production if the plant operated at rated capacity continuously [2]. The capacity factor takes into account maintenance downtime, unplanned outages, and reductions in output due to low water flows.
Putting it Together
The full hydropower equation in imperial units is:
Power (Watts) = Head (ft) x Flow (gallons/min) / 10.3
Where:
- Power is the power output in Watts
- Head is the net head of water in feet. Net head accounts for the gross head minus any head losses due to friction in pipes.
- Flow is the flow rate of water through the turbine in gallons per minute.
- 10.3 is a conversion factor when using imperial units of feet and gallons/min.
The equation is derived from the basic power equation and the potential energy of water:
Power = Force x Velocity
The force (F) on the water is equal to the weight of the water:
F = m x g
Where m is the mass of water and g is the gravitational acceleration constant.
The velocity (v) is the flow rate (Q) divided by the cross sectional area (A) of the penstock.
The mass (m) is equal to the density of water (p) multiplied by the volume (V). The volume is equal to the flow rate (Q) multiplied by the time (t).
Substituting into the power equation and re-arranging gives:
Power = p x Q x g x H / A
Where H is the net head in feet.
Converting the density and gravitational constant into appropriate imperial units gives the final equation.
(Sources: https://www.e-education.psu.edu/emsc297/node/648, https://www.waterandenergyconsulting.com/hydroview.pdf)
Real World Examples
One of the largest hydropower plants in the world is the Three Gorges Dam in China. It has a total generating capacity of 22,500 MW. According to the hydropower equation, the power output depends on the head, flow rate and efficiency. The Three Gorges Dam has an average head of 80 m, with a maximum flow rate of 116,000 m3/s. With an assumed efficiency of 90%, the power output can be calculated as:
Power = (Head x Flow Rate x Efficiency) / 11.81
Power = (80 x 116,000 x 0.9) / 11.81
Power = 22,732 MW
Another major hydropower installation is the Itaipu Dam, on the border between Brazil and Paraguay. It has an installed capacity of 14,000 MW. The dam has a head of 118 m and a flow rate of 40,000 m3/s. Again assuming 90% efficiency:
Power = (Head x Flow Rate x Efficiency) / 11.81
Power = (118 x 40,000 x 0.9) / 11.81
Power = 13,945 MW
This real world calculation matches closely with the installed capacity of 14,000 MW.