What Is The Change In Potential Energy Of Mass?
Definition of Potential Energy
Potential energy is the stored energy an object has due to its position or state. For example, a ball at the top of a ramp has gravitational potential energy due to the height of the ramp. A compressed spring has elastic potential energy due to its compressed state. In both cases, the potential energy is converted to kinetic energy as the ball rolls down the ramp or the spring expands.
Potential energy represents the work an object could potentially do as a result of its position or arrangement. It is stored energy that can later be released and converted into kinetic energy. The greater the potential energy, the greater the amount of energy that can be transformed into motion when released.
Formula for Potential Energy
The formula for gravitational potential energy measures the work needed to move an object to a higher location in a gravitational field. The formula is:
PE = mgh
Where:
- PE is the potential energy in joules (J)
- m is the mass of the object in kilograms (kg)
- g is the acceleration due to gravity (9.8 m/s2 on Earth)
- h is the height of the object above a reference point in meters (m)
This formula shows that an object’s potential energy increases linearly with its height. Doubling the height will double the potential energy. Furthermore, heavier objects require more work to lift against gravity, so potential energy is directly proportional to mass.
Examples of Potential Energy
There are many everyday examples of potential energy in our surroundings:
Book on a shelf
A book sitting on the edge of a shelf has gravitational potential energy. The higher up it is, the more potential energy it possesses since gravity can do more work on the book when it falls from a greater height.
Water behind a dam
Water held behind a dam has stored gravitational potential energy. The water can do work in turning turbines to generate electricity as it flows downhill through the dam. The greater the height of the water, the more potential energy it contains.
Object held above ground
Holding an object like a bowling ball at an elevated position stores gravitational potential energy in it. If released, the ball will accelerate downward under gravity, converting the potential energy into kinetic energy.
Conversion to Kinetic Energy
One of the most important aspects of potential energy is its ability to convert into kinetic energy. Kinetic energy is the energy of motion that an object possesses due to its velocity. The conversion between potential and kinetic energy occurs when an object that contains stored potential energy starts moving.
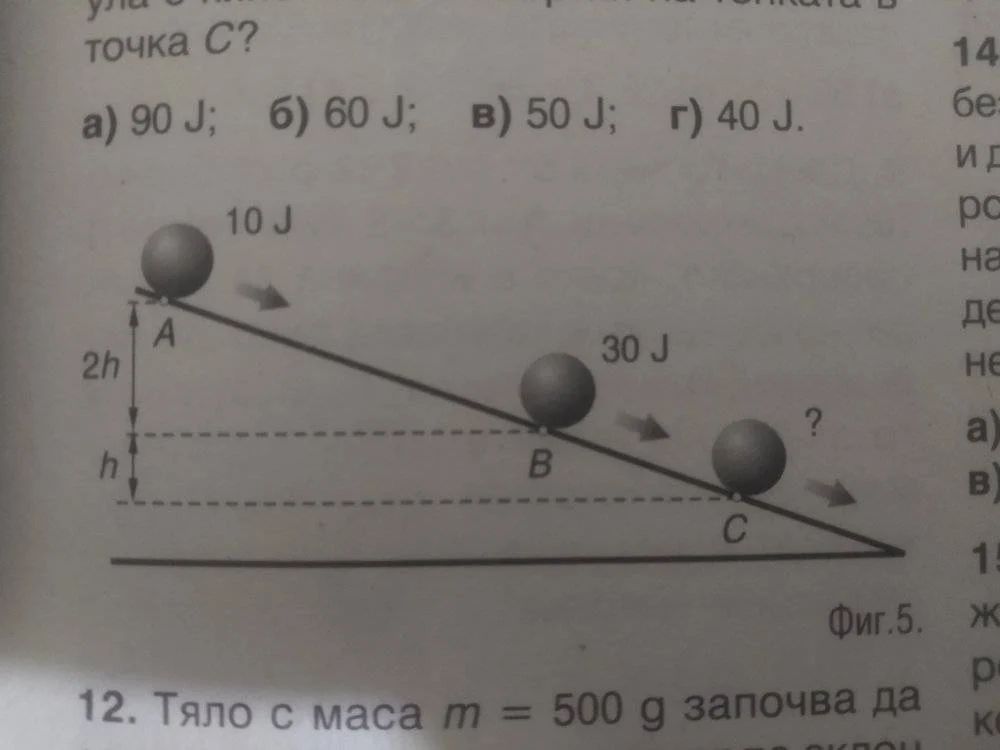
For example, consider a book placed at the edge of a table. The book contains potential energy due to its position relative to the floor. If the book falls off the table, the potential energy gets converted into kinetic energy as the book gains velocity and starts moving downwards. The kinetic energy continues increasing as the book accelerates under gravity until it hits the floor.
Another example is a pendulum. At the highest point of its swing, it contains maximum potential energy. As the pendulum swings down, the potential energy converts into kinetic energy and the pendulum gains speed. At the lowest point, the pendulum has minimum potential energy and maximum kinetic energy. As it swings upwards again, the kinetic energy converts back into potential energy.
This exchange between potential and kinetic energy occurs in everyday examples like falling objects, swinging pendulums, roller coasters going downhill, bows firing arrows, etc. The conversion enables the stored potential energy to be released and do work in the form of kinetic energy.
Conservation of Mechanical Energy
An important principle in physics is the conservation of mechanical energy. This means that the total mechanical energy in a closed system remains constant, even as energy transforms between potential and kinetic forms. Mechanical energy is the sum of an object’s kinetic energy and potential energy.
Kinetic energy is energy associated with motion. It depends on the mass and velocity of an object. Potential energy is stored energy that depends on an object’s position or shape. For example, a ball held at a height above the ground has gravitational potential energy due to its elevated position.
As the ball falls, its potential energy is converted into kinetic energy. Right before the ball hits the ground, almost all of the potential energy has become kinetic energy. The total mechanical energy at the start when the ball was held high is equal to the total mechanical energy at the end just before impact. Energy changes form between potential and kinetic, but the total amount of mechanical energy stays the same.
This conservation law applies to all closed systems, where no outside forces do work. Mechanical energy can transfer between objects in a system, but it cannot be created or destroyed. The principle of conservation of mechanical energy is a fundamental and widely useful concept in physics.
Potential Energy Graphs
A potential energy graph is a visual representation of how the potential energy of an object or system changes relative to position. On the graph, the vertical axis represents the amount of potential energy and the horizontal axis represents position. The height of the curve at any point indicates the magnitude of the potential energy at that position.
For example, when graphing the potential energy of an object relative to height above the ground, the curve will slope upwards. This indicates that as the height increases, the potential energy also increases. The curve may level off or even slope downwards at the peak height where the object has maximum potential energy.
Potential energy graphs allow you to visualize how potential energy changes as the position of an object or system is altered. The slope and shape of the curve provides important information about the forces and dynamics at work. Potential energy graphs are useful for analyzing mechanical systems and motions like oscillators, pendulums, and launched projectiles.
Comparing Potential Energies
When comparing the potential energies of different objects, the general rule is that objects at higher elevations have greater potential energy. This is because potential energy depends directly on an object’s height above some reference point, usually the ground.
For example, consider a book sitting on a tabletop versus a book held 2 meters above the floor. The book on the table has some potential energy relative to the floor, but the book held overhead has greater potential energy because it is at a higher elevation. If both books were to fall, the overhead book would accelerate faster and hit the ground with more kinetic energy because it started at a greater potential energy.
Another way to think about it is that more work would be required against gravity to lift the book overhead versus just placing it on the table. More work means more potential energy stored. So objects higher up can release more energy when falling, and therefore have greater initial potential energy.
This principle applies for any objects being compared side-by-side. Whether dealing with books, balls, buildings, or mountains, a higher elevation always correlates with greater gravitational potential energy.
Factors Affecting Potential Energy
The amount of potential energy that an object possesses depends on three key factors: mass, height, and gravitational field strength.
Mass – The more massive an object is, the greater its potential energy will be at a given height. Doubling the mass of an object will double its potential energy. This is because the potential energy formula includes mass as a variable.
Height – The higher an object is above the ground or a reference point, the greater its potential energy. Raising an object’s height will increase its potential energy. This is because height appears in the potential energy equation.
Gravitational Field Strength – The strength of the gravitational field determines how much potential energy an object will have at a given height. A stronger gravitational field means greater potential energy. On Earth the gravitational field strength is roughly 9.8 m/s2.
So in summary, the more massive an object, the higher its elevation, and the stronger the gravitational field, the more potential energy it will possess. These three variables allow us to calculate an object’s potential energy.
Applications of Potential Energy
Potential energy is extremely important for many scientific and engineering disciplines. Understanding how to calculate potential energy for different systems and objects allows us to predict motion, optimize design, and utilize energy more efficiently.
In engineering, knowledge of potential energy is key for modeling mechanical systems, structural design, and energy storage mechanisms. Engineers rely on potential energy concepts when analyzing stress and strain on materials, designing dams and energy storage tanks, and predicting system dynamics.
For physicists, potential energy forms a foundation for explaining motion, gravity, electricity, magnetism and more. Potential energy graphs help physicists visualize energy transitions and make calculations. Potential energy concepts are woven throughout major physics theories including classical mechanics, thermodynamics, and quantum mechanics.
Harnessing potential energy is also vital for energy production. Dams utilize the potential energy of water at high elevations to generate hydroelectric power. Similarly, compressed gas and chemical batteries store potential energy that can be released on demand. Understanding potential energy storage allows us to better capture, control, and utilize renewable energy sources.
Across science and engineering, grasping the nuances of potential energy is key for modeling how systems behave, designing more efficient technologies, and tapping into cleaner energy sources. Potential energy provides a powerful mental model for describing our physical world and enabling new innovations.
Importance and Usage
Potential energy is a fundamental concept in physics and engineering, playing an important role in understanding mechanical systems and processes. Here are some of the key applications and importance of potential energy:
Work and Power: The ability to do work on an object depends on transfers of potential energy. Power is defined as work done per unit time, which relies on potential energy converted into kinetic energy.
Conservation Laws: The total mechanical energy (potential + kinetic) of a closed system is conserved. This allows tracking energy transfers between potential and kinetic.
Dynamics: The forces acting on objects and resulting motion depend directly on gradients in potential energy (e.g. gravitational forces near Earth).
Energy Storage: Potential energy provides a means of storing energy for later use. For example, water behind a dam has gravitational potential energy that can be converted to electricity.
Orbital Motion: The orbits of planets and satellites are governed by a balance between kinetic energy and gravitational potential energy.
Chemical Energy: Energy stored in the bonds of atoms and molecules is a form of potential energy that can be released in chemical reactions.
In summary, potential energy is a foundational principle in physics that enables understanding many important phenomena and processes related to energy.