What Is Kinetic And Potential Sum?
Definition of Kinetic and Potential Energy
Kinetic energy is the energy an object possesses due to its motion. The faster an object moves, the more kinetic energy it has. Kinetic energy is directly proportional to the object’s mass and the square of its velocity. For example, a car moving at 60 mph has more kinetic energy than a car moving at 30 mph. The formula for kinetic energy is:
Kinetic Energy = 1/2 * mass * velocity^2
Potential energy is the stored energy an object has due to its position or chemical configuration. There are several types of potential energy including gravitational potential energy, elastic potential energy, chemical potential energy, and electrical potential energy. Gravitational potential energy is the energy stored in an object due to gravity. For example, a ball at the top of a ramp has gravitational potential energy that can be converted to kinetic energy as the ball rolls down. The formula for gravitational potential energy is:
Gravitational Potential Energy = mass * gravitational acceleration * height
The key difference between kinetic and potential energy is that kinetic energy is energy in motion while potential energy is stored energy due to an object’s position or chemical state. Kinetic and potential energy can convert back and forth from one form to another.
Examples of Kinetic Energy
Kinetic energy is the energy of motion. Some common examples of kinetic energy include:
- A moving car. The faster and more massive the car is, the more kinetic energy it has.
- A person walking or running. The kinetic energy increases as the person moves faster.
- Flowing water in a river. Faster moving water has higher kinetic energy.
- Wind. Faster blowing wind contains more kinetic energy.
The amount of kinetic energy depends on two variables – the mass (m) of the object, and the velocity (v) of the object. The relationship can be described by the formula:
Kinetic Energy = 1/2 * m * v^2
As the equation shows, if the mass or velocity increases, the amount of kinetic energy also increases. This is why a more massive object moving at the same speed as a lighter object will have more kinetic energy, and why moving faster increases kinetic energy even if the mass stays constant.
Examples of Potential Energy
Potential energy is stored energy that depends on an object’s position or shape. Some common examples of potential energy include:
A book sitting on a table has potential energy due to gravity. The higher the book is above the floor, the greater its potential energy. This gravitational potential energy depends on the book’s mass, the acceleration due to gravity, and the height of the book.
Water held behind a dam has potential energy due to its position. The water flows from high potential energy to low potential energy as it falls through the dam, converting that potential energy into kinetic energy. Again, the potential energy depends on the mass of water, gravity, and the height of the water behind the dam.
A stretched or compressed spring has potential energy due to its changed shape. The more a spring is compressed or stretched, the greater its potential energy. This elastic potential energy depends on the spring’s stiffness and how much it’s deformed from its relaxed state.
In each case, the potential energy stored in the object depends on its mass, height, shape, or position. This potential energy can be converted into kinetic energy if released, such as the book falling, water flowing, or spring uncoiling. Understanding potential energy helps explain many everyday phenomena.
Relationship Between Kinetic and Potential Energy
Kinetic and potential energy are able to convert back and forth between one another. This is because the total mechanical energy in a system remains constant, according to the law of conservation of energy. The kinetic and potential energies within the system can trade off, with one increasing as the other decreases, but the total amount of mechanical energy stays the same.
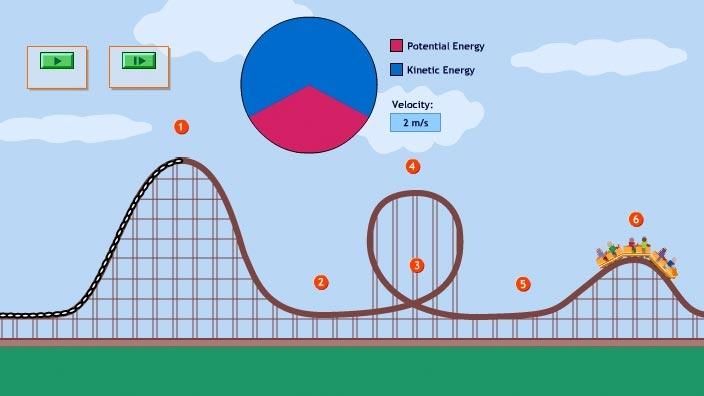
A classic example of this energy conversion is a roller coaster ride. At the top of a hill, the roller coaster has maximum potential energy but minimal kinetic energy. As it travels down the hill, it gains speed and kinetic energy while losing potential energy. At the bottom of the hill, the kinetic energy is maximized while the potential energy is minimized. As the coaster travels up the next hill, it slows down as the potential energy increases again and the kinetic energy decreases. This back and forth between kinetic and potential energy continues for the duration of the roller coaster ride, with the total mechanical energy remaining constant.
Other examples of kinetic and potential energy conversion include a pendulum swinging, a ball being thrown in the air, and a spring compressing and expanding. The transformation between these two forms of mechanical energy drives the motions we see in these systems.
Conservation of Mechanical Energy
The law of conservation of mechanical energy states that in a closed system, the total mechanical energy remains constant. This means that the sum of kinetic and potential energies does not change, even as energy is transferred between objects or converted from one form to another. For example, when a ball falls, its potential energy is converted to kinetic energy, but the total mechanical energy before and after the fall is the same.
This conservation applies to all closed systems, where no external forces do work. Even in complex mechanical systems with multiple interacting objects, the total initial mechanical energy and total final mechanical energy will be equal, as long as the system is closed. The conservation law is useful for analyzing mechanical systems and solving problems involving energy transfers and conversions. It simplifies calculations since the total mechanical energy remains unchanged.
Calculating Kinetic Energy
Kinetic energy is calculated using the following formula:
KE = 0.5mv2
Where:
- KE is kinetic energy in joules (J)
- m is mass in kilograms (kg)
- v is velocity in meters per second (m/s)
Let’s look at some examples of using this formula to calculate kinetic energy:
A car with a mass of 1500 kg is traveling at 20 m/s. To calculate its kinetic energy:
KE = 0.5 x 1500 x (20)2
= 0.5 x 1500 x 400
= 300,000 J
A tennis ball with a mass of 0.06 kg is served at a velocity of 35 m/s. Its kinetic energy is:
KE = 0.5 x 0.06 x (35)2
= 0.5 x 0.06 x 1225
= 36.75 J
As shown in these examples, the faster an object moves, the greater its kinetic energy. Kinetic energy increases exponentially with velocity.
Calculating Potential Energy
The formula for calculating gravitational potential energy is:
PE = mgh
Where:
- PE is the potential energy in joules (J)
- m is the mass in kilograms (kg)
- g is the acceleration due to gravity, 9.8 m/s2
- h is the height of the object in meters (m)
Let’s look at some examples of using this formula:
If a 5kg object is lifted 2 meters off the ground, the potential energy can be calculated as:
PE = mgh
= 5kg * 9.8 m/s2 * 2m
= 98 J
So the potential energy of lifting the 5kg object 2m is 98 J.
As another example, if a 12kg bicycle is lifted 4 meters off the ground, the potential energy is:
PE = mgh
= 12kg * 9.8 m/s2 * 4m
= 470 J
So lifting the 12kg bicycle 4m gives it 470 J of potential energy.
Real World Applications
Kinetic and potential energy concepts are used to understand the dynamics of many real world systems and mechanisms. Here are some common examples:
Roller Coasters: At the top of a hill on a roller coaster track, the roller coaster train has maximum potential energy due to its height above the ground. As the train descends, this potential energy gets converted into kinetic energy as the train speeds up. At the bottom of the hill, the train has maximum kinetic energy. The kinetic energy then starts converting back into potential energy as the train climbs the next hill.
Pendulums: A pendulum exhibits oscillations between kinetic and potential energy. At the maximum displacement, the pendulum bob has maximum potential energy. As the bob swings downwards, this potential energy converts into kinetic energy as it gains speed. At the bottom of the swing, the bob has maximum kinetic energy. This kinetic energy gets converted back into potential energy as the bob swings upwards again.
Springs: When a spring is compressed or stretched, it stores elastic potential energy. As the spring recoils, this potential energy converts into kinetic energy as the spring and attached object move. The kinetic energy then reconverts into potential energy as the spring compresses again, and the cycle repeats.
Hydroelectric Dams: The water stored behind the dam has potential energy due to its height above the turbines. As the water flows downwards through the dam, this potential energy gets converted into kinetic energy. The kinetic energy of the flowing water then turns the turbines to generate electricity.
Common Misconceptions
There are a few common misconceptions people have when learning about kinetic and potential energy:
One is confusing energy and force. Energy is the capacity to do work, while force is a push or pull on an object. Just because an object has energy does not mean there is an applied force on it. For example, a book sitting on a shelf has gravitational potential energy but there is no force acting on it.
Another misconception is that kinetic energy only applies to moving objects. This is not true – even objects at rest have kinetic energy at the molecular level due to the motion of their atoms and molecules. So all matter has some baseline amount of kinetic energy.
Additionally, some people believe that potential energy is stored inside an object. But potential energy is not contained within an object, it is stored within a system or configuration of objects. For example, the gravitational potential energy of a ball is not stored within the ball itself but depends on the ball’s height above the ground.
Finally, it’s important to understand that kinetic and potential energy are not distinct “types” of energy but are categories we use to describe energy flows and transformations. The total mechanical energy remains constant, even as energy is converted between kinetic and potential forms.
Conclusion
This article provided an overview of kinetic and potential energy, two of the most fundamental concepts in physics. We explored the definitions and real-world examples of each type of energy, as well as the close relationship between the two. The Principle of Conservation of Mechanical Energy states that the total mechanical energy in a closed system remains constant. This means that energy is never created or destroyed, only transformed between kinetic and potential forms.
Understanding the difference between kinetic and potential energy and how they convert between forms is key for analyzing mechanical systems. Whether it’s calculating the kinetic energy of a moving object or the potential energy stored in an object in relation to gravity, mastering these concepts allows prediction of motion, system behavior, and work performed. Real world applications range from the physics of sports and theme park rides to energy generation and storage.
In summary, kinetic and potential energy are fundamentals of physics and engineering, with broad importance across many fields. Grasping the conversion between the two forms provides insight into system dynamics and work. With the knowledge gained from this article, you are now well on your way to analyzing energy transfers in mechanical systems.