What Is Kinetic And Elastic Energy?
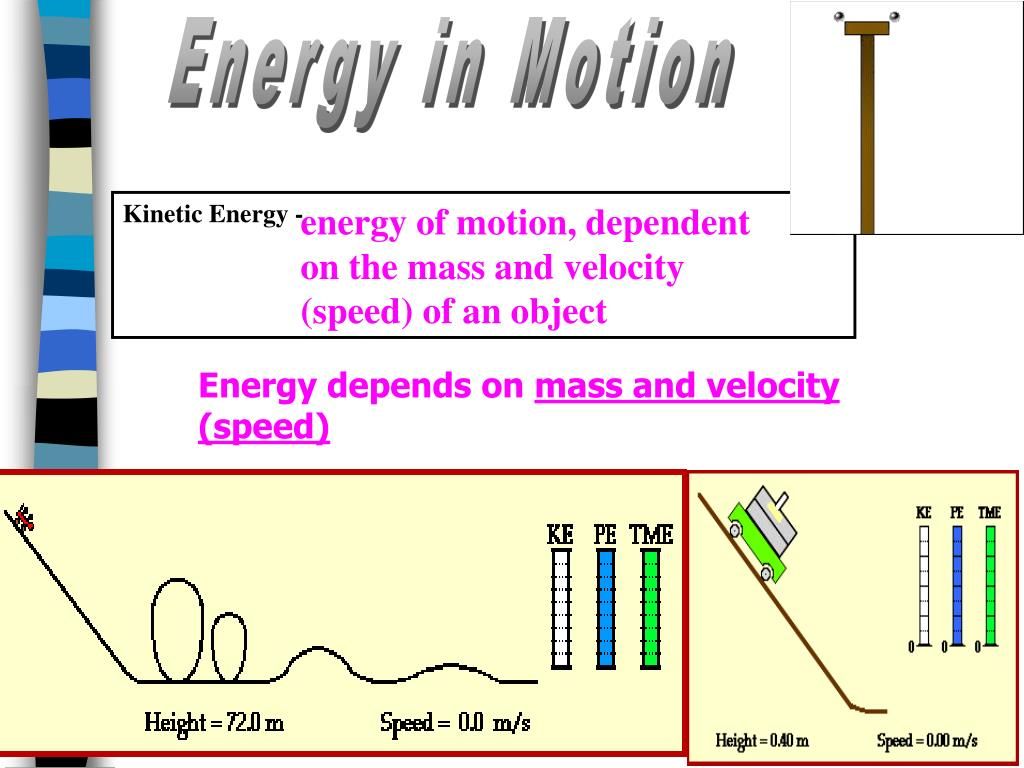
Kinetic energy and elastic potential energy are both important forms of mechanical energy. Mechanical energy is the energy possessed by an object due to its motion or position. Kinetic energy refers to the energy an object has due to its motion. Elastic potential energy refers to the potential energy stored in an elastic object when it is stretched or compressed. Understanding the difference between kinetic and elastic energy is key to understanding important physical concepts and solving problems in physics and engineering.
In this article, we will provide an in-depth explanation of kinetic and elastic potential energy. We will explore the definitions, formulas, and real-world examples of both types of mechanical energy. We will also discuss the interconversion between kinetic and elastic energy and highlight some key applications where these energy concepts are applied. By the end, you will have a strong grasp on these two forms of mechanical energy and how they relate to each other.
Kinetic Energy
Kinetic energy is the energy that an object has due to its motion. The faster an object moves, the more kinetic energy it has. Kinetic energy depends on two main factors:
Mass – The more massive an object is, the more kinetic energy it will have at the same velocity. Doubling an object’s mass doubles its kinetic energy.
Velocity – The faster an object moves, the more kinetic energy it has. Doubling an object’s velocity quadruples its kinetic energy.
The formula for kinetic energy is:
Kinetic Energy = 0.5 x Mass x Velocity2
Some examples of kinetic energy in everyday life include:
- A moving car
- A kicked soccer ball
- Water flowing in a river
- Wind turning the blades of a wind turbine
In each case, the faster the object is moving, the more kinetic energy it possesses. Kinetic energy allows cars to accelerate, balls to fly through the air, rivers to turn turbines, and wind to generate electricity. Understanding kinetic energy is key to understanding motion.
Formula for Kinetic Energy
The formula for kinetic energy is:
KE = 1/2mv^2
Where:
- KE = kinetic energy (in Joules)
- m = mass (in kilograms)
- v = velocity (in meters per second)
This formula shows that kinetic energy is proportional to the mass of an object and the square of its velocity. This means that as velocity increases, kinetic energy increases exponentially. For example, doubling the velocity of an object will quadruple its kinetic energy. This is because velocity is squared in the formula.
The reason kinetic energy increases so rapidly with velocity is that faster moving objects have more momentum. Greater momentum means more force is required to stop the object. This ability to do work and overcome resisting forces is what kinetic energy represents.
Examples of Kinetic Energy
Kinetic energy is present in many forms in everyday life and nature. Some common examples include:
Moving objects – Any object that is in motion, like a rolling ball, a car driving down the street, or a child swinging on a swingset, possesses kinetic energy. The amount of kinetic energy depends on the object’s mass and velocity.
Heat and thermal energy – At the atomic level, heat consists of the kinetic energy of rapidly vibrating and moving atoms and molecules. Higher temperatures mean the particles have more kinetic energy.
Sound – The kinetic energy of vibrating atoms and molecules gets transmitted through the air as waves, creating the sounds we hear. Louder sounds have greater kinetic energy.
Particles in Brownian motion – When observing small particles suspended in a gas or liquid under a microscope, we can see them moving about randomly due to collisions with atoms and molecules. This Brownian motion is caused by transfers of kinetic energy.
Flowing liquids and gases – Fluids like water flowing down a stream or wind blowing contain kinetic energy due to the movement and collisions of their particles.
Chemical reactions – Kinetic energy is released when chemical bonds are formed and broken during chemical reactions. Exothermic reactions that give off heat involve releases of kinetic energy.
Light – According to quantum physics, light travels in the form of particles called photons that have kinetic energy proportional to their frequency/color.
Elastic Potential Energy
Elastic potential energy is energy stored in elastic materials as a result of deformation or change in shape. Elastic materials, such as rubber bands, springs, and bungee cords, have the ability to return to their original shape after being stretched or compressed. The energy gets stored in the deformed shape and is released when the material returns to its resting position.
A common example of elastic potential energy is a stretched rubber band. As you stretch the rubber band, you are doing work against the restorative force of the rubber molecules, storing energy in the stretched rubber band. When you let go, the rubber band snaps back to its original shape, releasing the stored elastic potential energy.
Another example is a compressed spring. Compressing or squeezing a spring requires force to work against the spring’s elasticity. This stores elastic potential energy in the compressed spring. Releasing the spring allows it to expand to its relaxed length, converting the stored energy into kinetic energy.
Bungee cords also demonstrate elastic potential energy. When you stretch a bungee cord, the elastic material stores energy. The stored energy gets transferred into kinetic energy as the bungee jumper falls and the cord rebounds to its original length.
Formula for Elastic Potential Energy
The formula for elastic potential energy is:
Ep = 1/2kx2
Where:
- Ep is the elastic potential energy
- k is the spring constant
- x is the amount of deformation or displacement
The elastic potential energy depends on two variables – the spring constant k and the deformation or displacement x. The spring constant k is a measure of the stiffness of the spring. A larger k value indicates a stiffer spring. The deformation x refers to how much the spring is stretched or compressed from its natural relaxed length.
As seen in the formula, the elastic potential energy is directly proportional to the square of the deformation x. This means doubling the deformation will quadruple the elastic potential energy. The energy increases exponentially with deformation. The energy is also directly proportional to the spring constant k. Stiffer springs with higher k values will store more energy for the same amount of deformation.
In summary, the elastic potential energy of a spring depends on how stiff the spring is (k) and how much it is deformed (x). The energy increases exponentially with deformation and linearly with spring stiffness.
Examples of Elastic Potential Energy
Elastic potential energy can often be seen in springs, bungee cords, stretched rubber bands, and other objects that can stretch or compress. Some examples include:
– A compressed spring contains elastic potential energy. When released, the spring converts the stored energy into kinetic energy as it extends and returns to its natural length.
– Stretching a bungee cord or rubber band stores elastic potential energy. The molecules in the material are stretched from their relaxed positions, giving them potential energy that can do work when released.
– Trampolines also demonstrate elastic potential energy. As a person bounces, they compress the springs in the trampoline mat. The springs then convert the energy into kinetic energy to bounce the person upwards again.
– Pulling back on a bow stores elastic potential energy in the bending of the bow material. Releasing the arrow transfers this energy into kinetic energy.
– Pogo sticks and jump stilts work by building up elastic potential energy in springs as the user presses down. The energy is released to propel the user upwards.
– Suspension bridges and buildings absorb wind energy by the elastic stretching of cables and other structural components. The materials act like giant springs storing energy.
In all these examples, the elastic potential energy builds up in the deformation of the material. When released, the object can revert to its original shape and transfer the energy into motion.
Conversions Between Kinetic and Elastic
One of the most important relationships between kinetic and elastic potential energy is that they can readily convert back and forth between each other. This conversion allows for oscillations and vibrations which are central to many mechanical systems.
A classic example demonstrating the conversion between kinetic and elastic potential energy is a bouncing ball. As gravity accelerates the ball downward, it gains kinetic energy. When the ball hits the floor and compresses, that kinetic energy gets temporarily converted into elastic potential energy stored in the deformation of the ball. As the ball rebounds upwards, the elastic potential energy is converted back into kinetic energy. This cycle repeats itself with some loss of energy each bounce.
Another common example is a mass attached to a spring system. When the spring is compressed or extended, it stores elastic potential energy. If released, the spring converts this into kinetic energy of the mass. As the mass oscillates back and forth, kinetic energy is converted into potential and vice versa in a harmonic fashion. This basic spring-mass system is key to understanding vibration absorption systems and resonances.
Being able to understand and quantify the continuous interconversion between kinetic and elastic potential energy is key to analyzing the dynamics of bouncing, oscillating, vibrating, and wave propagation phenomena. This interchange allows energy to be stored, released, and transferred between different mechanical modes.
Applications and Importance of Kinetic and Elastic Energy
Kinetic and elastic potential energy play important roles in many real-world applications and technological systems. Understanding how to utilize these forms of mechanical energy provides opportunities for innovation and improving efficiency.
One key application is energy storage. Kinetic energy can be stored in the rotation of flywheels, while elastic potential energy can be stored in compressed springs and stretched elastic materials. These stored mechanical energies can then be harnessed to perform useful work.
Regenerative braking is another important application involving the interconversion of kinetic and elastic energy. In electric vehicles, the kinetic energy of the moving car is converted into elastic potential energy in a spring when braking. This elastic energy is then used to recharge the car’s battery.
Amusement park rides utilize kinetic and elastic potential energies to excite and thrill passengers. Rollercoasters convert gravitational potential energy into kinetic energy, while bungee jumps and trampolines exemplify the interplay between elastic potential and kinetic energies.
Understanding these mechanical energy concepts allows engineers to design more efficient systems that waste less energy, utilize energy recycling, reduce costs, and develop innovative solutions. Kinetic and elastic energies play integral roles in physics and energy sciences.
Summary
Kinetic energy and elastic potential energy are two types of mechanical energy that are often converted between one another. Kinetic energy is the energy of motion and depends on an object’s mass and velocity. The formula for kinetic energy is KE=1/2mv^2. Examples include a moving vehicle or a falling object. Elastic potential energy is stored energy in an elastic material that is stretched or compressed. The formula is PE=1/2kx^2 where k is the spring constant and x is the displacement. Examples include a stretched bungee cord or a compressed spring. These types of energy can easily convert back and forth, such as when a bouncing ball converts kinetic energy to elastic potential energy as it compresses on impact, then back to kinetic energy as it rebounds. Understanding the basic principles of kinetic and elastic energy allows us to apply them in the design and function of many machines and mechanical devices that are an important part of our modern world.
The key takeaways are:
– Kinetic energy depends on an object’s mass and velocity
– Elastic potential energy depends on the spring constant and displacement of an elastic material
– These types of mechanical energy can readily convert between forms
– Applications and devices rely on these conversions for functionality