What Are The Units For Specific Mechanical Energy?

Specific mechanical energy is a concept used in physics and engineering to describe the total mechanical energy per unit mass in a system. It represents the sum of a system’s kinetic and potential energy. Specific mechanical energy is typically measured in units that combine distance and force.

There are several different unit systems used to measure specific mechanical energy. The most common ones are SI units (meters and Newtons), CGS units (centimeters and dynes), and English engineering units (feet and pounds). The choice of units depends on the country and field of application. It’s important to understand how to properly convert between the different units when working with specific mechanical energy calculations.

Table of Contents

SI Units

The standard SI units for specific mechanical energy are joules per kilogram (J/kg) and meters squared per second squared (m2/s2). The joule is the SI unit for energy, while kilograms measure mass. So joules per kilogram gives us energy per unit mass, which is the definition of specific mechanical energy.

Meters per second squared is also commonly used, since it represents velocity squared. Kinetic energy is equal to 1/2mv^2, so velocity squared gives us kinetic energy per unit mass. Therefore, meters squared per second squared is equivalent to joules per kilogram as a measure of specific mechanical energy.

CGS Units

In the CGS system, the units for specific mechanical energy are ergs per gram (erg/g) or centimeters squared per second squared (cm2/s2). The CGS system is older than the SI system and was commonly used in science and engineering fields until the 1970s. In the CGS system:

The unit of energy is the erg, which equals 10^-7 joules.

The unit of mass is the gram.
The unit of length is the centimeter.
The unit of time is the second.

So in CGS units, specific mechanical energy would be expressed in ergs per gram (erg/g). This is found by taking the energy in ergs and dividing by the mass in grams. It could also be expressed in cm2/s2 by taking the energy and dividing by the mass.

The CGS system is not commonly used today outside of specialized scientific contexts. SI units like joules per kilogram (J/kg) are more standard for expressing specific mechanical energy.

English Engineering Units

In English engineering units, the most common units used for specific mechanical energy are foot-pounds force per pound mass (ft·lbf/lbm) and feet squared per second squared (ft2/s2).

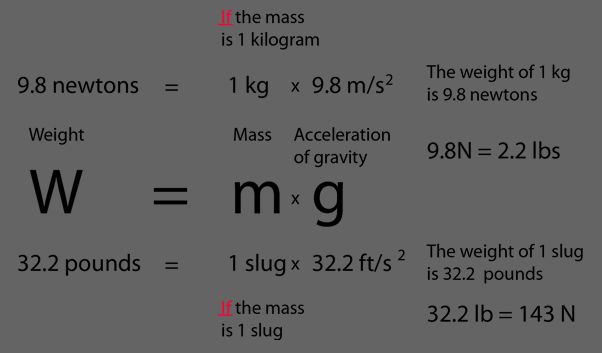
Foot-pounds force per pound mass (ft·lbf/lbm) is defined as the amount of energy needed to lift one pound of mass vertically one foot against gravity. This unit is commonly used in mechanical and structural engineering calculations involving energy, work, power, and torque.

Feet squared per second squared (ft2/s2) is the unit for kinetic energy in English engineering units. Kinetic energy is proportional to the mass and the square of the velocity, so the units are mass (slugs) multiplied by velocity squared (ft2/s2). This unit allows convenient calculation of kinetic energy for systems measured in feet, seconds, and slugs.

Converting Between Units

When working with specific mechanical energy, you may need to convert between different unit systems. Here are some useful conversion factors:

1 J = 1 kg m2/s2
1 erg = 1 g cm2/s2
1 ft lbf = 1.3558 J

For example, to convert 10 J to ergs:

10 J x (1 kg m2/s2) / (1 g cm2/s2) = 10,000 erg

To convert 50 ft lbf to Joules:

50 ft lbf x 1.3558 J/ft lbf = 67.79 J

Care must be taken when converting between units to ensure the conversion factors are applied properly. Having a solid understanding of the relationships between the various unit systems is critical for working with specific mechanical energy calculations.

Using Specific Mechanical Energy

Specific mechanical energy is commonly used in physics and engineering when analyzing systems where energy is transferred between potential and kinetic forms. Calculating the total specific mechanical energy at any point in the system allows you to solve many types of problems.

One major application is solving conservation of energy problems. If we know the specific mechanical energy at two different points in a system, conservation of energy states that these values must be equal (in the absence of nonconservative forces like friction). For example, we can calculate the specific mechanical energy of a ball at the top of a ramp based on its height and speed. Then calculate it again at the bottom of the ramp using the new height and speed. Setting them equal allows us to determine information we didn’t know before, like the speed at the bottom.

Specific mechanical energy is useful because it combines potential and kinetic energy into one simple metric. By tracking how this value changes between different system points, we gain insights into how energy transforms within the system while obeying the conservation of energy law.

Specific Mechanical Energy in Physics

In physics, specific mechanical energy is defined as the sum of a system’s kinetic and potential energies per unit mass. It represents the amount of energy associated with the motion and position of an object or particles within a system.

Kinetic energy is energy associated with motion. The kinetic energy of an object depends on its mass and velocity. Potential energy is stored energy associated with an object’s position or configuration. For example, a ball at the top of a ramp has gravitational potential energy due to its height above the ground.

The concept of specific mechanical energy helps relate the kinetic and potential energies of a system at different points. As an object’s potential energy decreases, its kinetic energy will increase by the same amount (ignoring nonconservative forces like friction). The total mechanical energy remains constant. This reflects the conservation of energy principle.

Specific mechanical energy is directly connected to the physics concept of work. When net work is done on an object, its specific mechanical energy changes. For example, lifting a ball against gravity does positive work, increasing its potential energy. Letting it roll down the ramp does negative work, converting that potential energy into kinetic energy.

The specific mechanical energy at any point provides critical information about how much work would be required to move an object to a new position or velocity within the system.

Specific Mechanical Energy in Engineering

Specific mechanical energy has many important applications in engineering and mechanical systems. Engineers often perform energy balances to analyze the flow of energy in a system. They track how much energy enters, exits, stores, or converts from one form to another. The specific mechanical energy at different points reveals insights into a system’s efficiency.

For example, in a hydraulic turbine system, the water’s initial gravitational potential energy gets converted into kinetic energy and eventually electrical energy via the turbine. By calculating the specific mechanical energy at the inlet and outlet, engineers can determine how much energy was lost to friction, noise, and other inefficiencies. This helps optimize the system design and operations.

Another common use is evaluating efficiency in pump and turbine designs. The specific mechanical energy change between the inlet and outlet determines how much useful energy transfer occurred versus lost energy. Engineers aim to maximize efficiency by minimizing energy losses. Careful calculations using specific mechanical energy help identify areas for efficiency improvements.

Overall, tracking specific mechanical energy flows provides critical data for analyzing and optimizing systems. It gives quantitative insights into where energy is used versus wasted. This allows engineers to improve efficiency, reduce costs, and design higher-performing systems.

Common Confusions

Specific mechanical energy is sometimes confused with other concepts and quantities in physics and engineering due to the similarity in terminology. Two of the most common confusions are:

Mistaking Units for Types of Energy

The term “specific mechanical energy” refers to energy per unit mass. The word “specific” indicates we are talking about units. However, some people mistakenly interpret “specific mechanical energy” as a particular form or type of mechanical energy, rather than just a quantity expressed in units per mass.

Mixing Up with Mechanical Power

Because “specific mechanical energy” contains the word “mechanical,” some mix it up with mechanical power. However, they are completely different quantities – power is the rate at which work is done, while specific mechanical energy is the amount of potential and kinetic energy per unit mass. The units are different too, power is in Watts while specific mechanical energy is in Joules/kg.

Conclusion

In summary, the key units for specific mechanical energy are joules in the SI system, ergs in the CGS system, and foot-pounds in the English engineering system. Though these units may seem disparate, it is important to be able to convert between them as needed. Specific mechanical energy is an important concept in physics, engineering, and other technical fields, so properly tracking and calculating units is essential.

Using the right units for specific mechanical energy ensures calculations are performed accurately. Converting between unit systems enables effective communication between different disciplines and countries. While memorizing conversions takes initial effort, the payoff in precise computations and shared understanding makes it well worth the investment. With some practice, unit conversions can become second nature. By properly applying the units discussed here for specific mechanical energy, one can reliably carry out and report on quantitative work.