Why Does A Spring Gain Potential Energy?

Potential energy is the stored energy an object has due to its position or shape. A spring is an elastic object that can be compressed or extended from its resting position. When a spring is compressed or extended, it gains potential energy. This potential energy is a result of the elasticity of the spring and is described by Hooke’s Law.

Hooke’s Law states that the force needed to compress or extend a spring is proportional to the distance the spring is displaced from its resting position. The further a spring is compressed or extended, the more force is required to continue the displacement. This force x distance determines the work done on the spring, which is stored as potential energy.

Elastic Potential Energy

When an object like a spring is compressed or stretched from its natural state, it gains potential energy. This type of stored energy that results from the deformation of an elastic object is called elastic potential energy.

For example, when you stretch or compress a spring, you are doing work against the spring’s restorative force. The energy gets stored in the spring as potential energy. When the external force is released, the spring converts the potential energy into kinetic energy as it returns to its original shape.

The same thing applies for other elastic materials like rubber bands. By stretching or compressing them, you store energy in their deformation. Once released, this potential energy converts into motion. So elastic potential energy refers to the stored energy in any elastically deformed object due to its change in shape or configuration.

Hooke’s Law

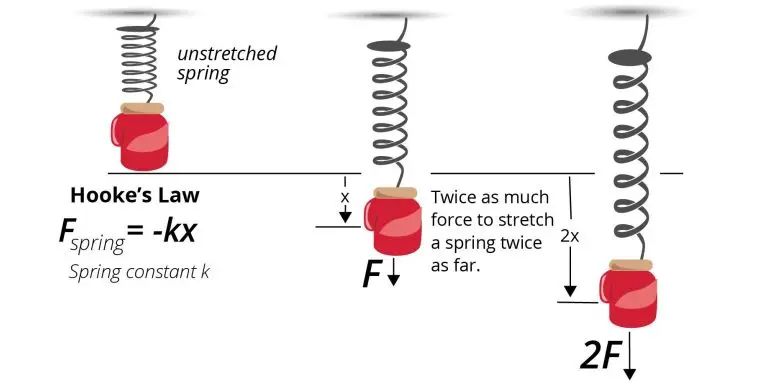
Hooke’s law is a principle in physics that states that the force (F) needed to extend or compress a spring by some distance (x) is proportional to that distance. The law is named after 17th-century British physicist Robert Hooke.

Mathematically, Hooke’s law is expressed as:

F = -kx

Where:

• F is the force exerted by the spring
• x is the displacement of the spring from its equilibrium position
• k is the spring constant that is characteristic of the spring

The minus sign indicates that the force exerted by the spring is in the opposite direction of the displacement. For example, if the spring is stretched, the restoring force will be in the opposite direction, acting to bring it back to its original length.

The spring constant k depends on the material and construction of the spring. The stiffer the spring, the greater the value of k and the stronger the restoring force it exerts for a given displacement.

Hooke’s law implies that the extension or compression of a spring is directly proportional to the force applied to it. This linear relationship only holds up to a certain point, however. If the displacement is too large, the spring will no longer obey Hooke’s law and will become permanently deformed.

Work Done on a Spring

When an external force is applied to a spring to either stretch or compress it, the spring responds with an opposing restoring force. This restoring force acts against the direction of the external force. As the external force displaces the spring from its natural equilibrium position, it must do work against the restoring force of the spring.

The amount of work done on the spring is calculated as the product of the force applied (F) and the distance the spring is displaced (dx). Mathematically, the work done is:

W = F * dx

Where W is the work done, F is the external force applied, and dx is the distance the spring is stretched or compressed. This work done on the spring by the external force is stored in the spring as potential energy.

As more work is done to further displace the spring, more potential energy builds up. When the external force is removed, the stored potential energy is converted back into kinetic energy as the spring returns to its original shape.

So in summary, external work is done on a spring when a force displaces the spring from its equilibrium position. This transfers energy into the spring, allowing it to store potential energy.

Energy Stored in a Spring

When a spring is stretched or compressed, energy is stored in the deformation of the coils. This energy comes from the work done in displacing the spring from its relaxed position. The potential energy stored in a spring can be calculated using the equation:

PE = 1⁄2 kx2

Where:

• PE is the potential energy stored in joules (J)
• k is the spring constant in newtons per meter (N/m)
• x is the displacement from the spring’s relaxed position in meters (m)

The 1⁄2 comes from the integration of Hooke’s law, which states that the force needed to compress or extend a spring is proportional to the displacement. By integrating force over distance, we get the work done on the spring, which equals the stored potential energy.

So in summary, the potential energy stored in a compressed or extended spring depends on the spring constant k, and increases quadratically with displacement x from the relaxed position.

Real-World Examples

Springs are found in many everyday objects and play an important role in storing elastic potential energy. Here are some examples:

Trampolines – The springs under the trampoline bed store energy as you press down on the fabric. This energy is then released to launch you in the air.

Pogo sticks – Much like a trampoline, the spring inside the pogo stick gets compressed as you push down on it with your body weight. The spring then expands and provides an upwards force to make you bounce.

Slinkies – When you stretch or compress a slinky, you are doing work to store energy in the coiled spring. Letting go allows the slinky to return to its equilibrium position as the energy is released.

Car suspensions – Springs and shock absorbers in the suspension system of cars and trucks compress and expand to absorb bumps in the road. This cushions the ride for passengers by storing and releasing energy.

Mousetraps – The spring arm is bent back to store energy and then released to snap shut the hammer part that traps mice.

Mattresses – Mattress springs compress under your weight as you lay down and then spring back when you get up, reducing pressure points.

Compression vs Extension

When comparing potential energy stored in compressed versus extended springs, the key factor is the change in length from the spring’s natural unstretched length. According to Hooke’s law, the force needed to compress or extend a spring is proportional to the displacement from its equilibrium length. This means whether a spring is compressed or extended, the energy stored depends on how much it has been displaced, not the direction of displacement.

For example, compressing a spring by 5 cm stores the same amount of potential energy as extending the same spring by 5 cm. The energy comes from the work done against the spring’s restoring force. When compressed, the restoring force is directed outward as the spring tries to expand. When extended, the restoring force is directed inward as the spring tries to contract. But in both cases, the magnitude of the force and displacement are identical for the same change in length.

The potential energy stored can be calculated using the equation PE=1/2kx^2, where k is the spring constant and x is the displacement from equilibrium. The direction of displacement does not matter, only the magnitude. Therefore, springs store equal potential energy for equal compression or extension. The energy gets converted back to kinetic energy if released.

Factors Affecting Potential Energy

The amount of potential energy stored in a spring depends on two key factors – the spring constant and the displacement or compression/extension of the spring.

The spring constant (k) measures the stiffness of the spring. A higher spring constant means the spring is stiffer and more resistant to compression or extension. The stiffer the spring, the more force required to compress or extend it, and thus the more potential energy that can be stored.

The displacement (x) refers to how much the spring is compressed or extended from its equilibrium position. The greater the displacement, the more potential energy stored in the spring. This is because more work is done to compress or extend the spring from its natural length.

The potential energy (PE) stored in a spring can be calculated using the equation: PE= 1⁄2kx2. Where k is the spring constant and x is the displacement. This shows that the energy stored is directly proportional to the square of the displacement and the spring constant.

In summary, stiffer springs and greater displacement results in more potential energy stored. The energy is stored in the coils and released when the spring recoils back to its original shape.

Conservation of Energy

When a spring oscillates between compression and extension, the energy converts between kinetic energy and potential energy. This is an example of the conservation of energy in action.

At the maximum compression or extension points, the spring has maximum potential energy and zero kinetic energy since it has momentarily stopped moving. As the spring starts to move back towards its equilibrium position, it gains kinetic energy as the potential energy is converted to kinetic. At the midpoint, the spring has maximum kinetic energy and zero potential energy.

This back and forth transfer of energy between potential and kinetic continues with each oscillation. The total amount of energy remains constant, oscillating between potential and kinetic. Energy is never lost, only converted between forms. This principle is known as the conservation of energy.

Friction and air resistance will slowly dissipate some of the energy over time. But in an ideal frictionless system, the total energy remains fixed. The conservation of energy is why a spring can continue oscillating for a long time before coming to rest.

Conclusion

In summary, springs are able to store potential energy due to their elastic properties. When a spring is stretched or compressed, the atoms are forced closer together or further apart. This deformation creates an elastic potential energy that gets stored in the spring. The amount of potential energy stored depends on the spring constant and how much the spring has been displaced from its relaxed position. This potential energy can then be converted into kinetic energy if the spring is allowed to return to its original shape. Understanding the ability of springs to store elastic potential energy helps explain many common examples, from bounce houses to pogo sticks. The compression and extension of springs provides a simple way to accumulate energy that can later be released to perform work.