Why Can We Define Potential Energies?

Potential energy is defined as stored energy that an object has due to its position or due to the arrangement of its parts. Being able to define and calculate potential energies for different situations is critically important in physics and engineering because it allows us to mathematically describe how energy flows between objects. Having a precise definition of potential energy is the foundation for analyzing mechanical systems and for discovering the conservation of energy.

Potential energy represents possibility. An object high up has the potential to do work as it falls, so we can define its gravitational potential energy. A compressed or stretched spring has the potential to do work as it relaxes, so we define the spring’s elastic potential energy. Without these defined potential energies, we could not fully describe mechanical systems and predict their behavior using equations. Defining potential energies is key to unlocking the powerful mathematical framework of physics.

Forms of Potential Energy

There are several common forms of potential energy that are important to understand:

Gravitational Potential Energy

Gravitational potential energy depends on the mass of an object, its height above a reference point (such as the ground), and the strength of gravity. When an object is lifted upwards, it gains gravitational potential energy. This energy can later be released as kinetic energy when the object falls.

Elastic Potential Energy

Elastic potential energy arises when objects are compressed or stretched. For example, when a spring is compressed or stretched away from its relaxed length, the spring stores elastic potential energy. This energy can be released to do work when the spring recoils.

Chemical Potential Energy

Chemical potential energy is stored in the bonds between atoms and molecules. Chemical reactions can release this potential energy, such as in batteries or when fuels are burned.

Electrical Potential Energy

Electrical potential energy depends on the electric charge and voltage between two points. It is stored in capacitors and can be released to power electrical devices.

Calculating Potential Energy

Potential energy can be calculated using equations that depend on the type of potential energy involved. Here are some of the main potential energy equations and examples of calculating potential energy using them:

Gravitational Potential Energy

Gravitational potential energy depends on an object’s mass, the acceleration due to gravity, and the object’s height above a reference point. It’s calculated using:

PE_grav = mgh

Where m is mass, g is acceleration due to gravity, and h is height. For example, calculating the gravitational potential energy of a 5kg object lifted 2m off the ground, with g=9.8m/s²:

PE_grav = (5kg)(9.8m/s²)(2m) = 98 J

Elastic Potential Energy

Elastic potential energy depends on the spring constant of an elastic object and how much it’s been stretched or compressed. It’s calculated using:

PE_elastic = 1/2 kx²

Where k is the spring constant and x is the displacement distance. For example, calculating the elastic potential energy of a spring with k=100 N/m stretched 0.3m:

PE_elastic = 0.5(100 N/m)(0.3m)² = 4.5 J

Relationship to Kinetic Energy

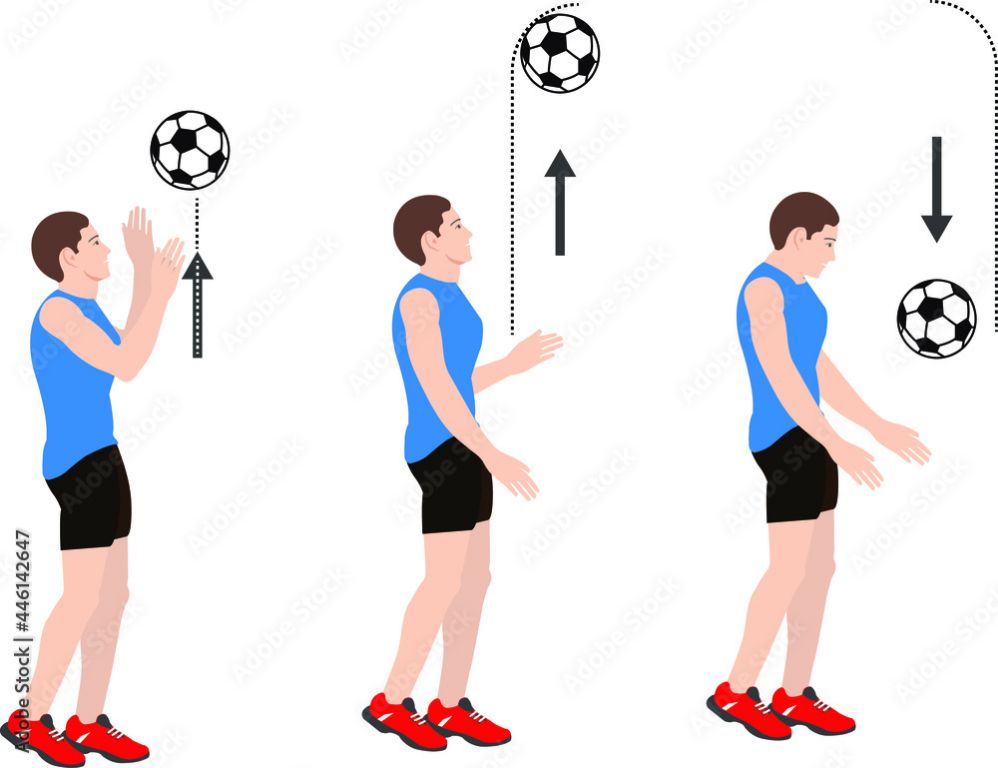
Potential energy and kinetic energy are two forms of mechanical energy. The basic principle connecting the two is the law of conservation of energy, which states that energy cannot be created or destroyed, only converted from one form to another. This means that potential energy can be converted into kinetic energy and vice versa within a closed system.

Some common examples of potential energy being converted into kinetic energy include:

• A rock at the edge of a cliff has potential energy due to gravity. When it falls, this potential energy gets converted into kinetic energy, causing the rock to accelerate towards the ground.
• A compressed or stretched spring has potential energy. When released, the potential energy converts into kinetic energy as the spring returns to its resting position.
• Water held behind a dam has potential energy. When released through the dam, the water falls and flows, converting that potential energy into kinetic energy.
• Chemical potential energy stored in fuels and food can be converted into kinetic energy through combustion or metabolic processes.

The interplay between potential and kinetic energy underlies all motion and is a fundamental concept across many fields of physics and engineering. Understanding the relationship between these two forms of energy unlocks a deeper insight into how nature works.

Conservation of Energy

A key principle in physics is the law of conservation of energy. This states that the total mechanical energy in a closed system remains constant. Mechanical energy refers to the sum of kinetic energy and all forms of potential energy in a system.

While energy can change form, the total amount of mechanical energy is always conserved. For example, a ball at the top of a ramp has gravitational potential energy. As the ball rolls down the ramp, this potential energy gets transformed into kinetic energy, increasing the velocity of the ball. However, the total mechanical energy before and after remains the same.

Potential energy can also transfer between different types, while the total potential energy remains constant. For instance, when stretching a spring, elastic potential energy increases. But compressing the spring then transforms this back into kinetic energy without any net change in mechanical energy. The conservation of energy is a fundamental law of physics that applies to all closed systems.

Potential Energy Curves

Potential energy curves, also known as potential energy surfaces, are graphical representations of how the potential energy of a system changes with position. They are useful for visualizing how potential energy relates to the structure and stability of molecules, atoms, and other systems.

To create a potential energy curve, the potential energy is plotted on the y-axis while the position variable is plotted along the x-axis. This position variable could be the distance between atoms in a molecule, the displacement of a spring from its equilibrium position, the angle between chemical bonds, etc.

The shape of the curve reveals key information. Slopes indicate the force acting at that position, and minima (low points) represent stable configurations where the system has lower potential energy. Systems tend to gravitate toward these minimal energy orientations. The depth of the minima quantifies the stability – deeper minima correspond to more stable arrangements.

Potential energy curves allow us to model molecular processes like chemical reactions. As atoms undergo collisions or rearrangements, they traverse the energy landscape, moving through higher energy transition states before settling into lower energy stability. Understanding these curves helps predict and describe the structure and behavior of matter.

Applications

Potential energy concepts are used extensively in physics, chemistry, engineering, and other sciences. Here are some practical examples of how potential energy is applied:

Physics: Gravitational potential energy helps explain orbits and satellite motion. Electric potential energy is used in circuits and electrical components. Spring potential energy applies to springs, elastic bands, and other elastic materials.

Chemistry: The concept of potential energy surfaces allows chemists to model chemical reactions and understand reaction dynamics. Potential energy curves help describe molecular structures and chemical bonds.

Engineering: Engineers use potential energy equations to analyze stressed materials and design stable structures. Potential energy stored in reservoirs provides hydroelectric power generation. Engineers optimize potential and kinetic energy flows in mechanical systems.

Biology: ATP molecules store chemical potential energy that is released to power cellular processes. The 3D shapes and functions of proteins and DNA are governed by potential energies.

These are just a few examples. Potential energy is a fundamental concept running through many scientific and engineering fields, with widespread practical applications.

Limitations

While potential energy is a useful concept in classical physics, there are some limitations to its definition and applications:

Defining the zero point of potential energy is arbitrary – often we set the zero point at infinity or when particles are completely separated. But this assumes particles can separate infinitely, which may not reflect real physical systems.

Calculating potential energy relies on models like the gravitational force or spring force equations. These are approximations and can break down at small scales or high energies.

Potential energy doesn’t account for phenomena described by quantum mechanics or relativity. At very small scales, particle energies are quantized and continuous potential energy curves no longer accurately describe dynamics.

The conservation of energy law can be violated in certain scenarios in modern physics, like radioactive decay. Potential energy curves may not give accurate predictions in these situations.

Defining potential energy requires assuming isolated systems with conservative forces. But real systems interact with their environment in complex ways, limiting this simplifying assumption.

While a useful classical approximation, potential energy has limitations at extreme scales and when quantum, relativistic, or open system effects become relevant.

Advanced Concepts

Our discussion of potential energy so far has focused on the classical physics treatment. However, quantum mechanics and relativity reveal fascinating new insights into potential energy.

In quantum mechanics, the potential energy function is used to solve the Schrödinger equation to determine the allowed energy states of a particle or system. Rather than a single defined potential energy, the particle can occupy different quantized energy levels. The solutions show probabilities and wavefunction amplitudes rather than definite values. Quantum tunneling allows particles to pass through potential barriers if there is a non-zero probability amplitude on the other side.

Relativistic effects become important when dealing with particles moving at speeds comparable to the speed of light. The relativistic energy includes an increase in mass as the particle’s velocity increases. This modifies the kinetic energy term and also adjusts the potential energy at high speeds. Relativistic potential energy must be used when analyzing interactions between subatomic particles, providing small but significant corrections to the classical potential energy equations.

Conclusion

In summary, potential energy is an extremely useful concept for understanding and predicting the behavior of physical systems. By calculating the potential energy stored in an object or system due to its position, configuration, or composition, we gain key insights into its dynamics and interactions.

Some of the key points regarding potential energy covered in this article include:

• Potential energy exists in multiple forms, such as gravitational, elastic, chemical, and electrical.
• The potential energy of a system can be quantitatively calculated using equations related to the specific form.
• Changes in potential energy are directly tied to changes in kinetic energy based on the conservation of energy.
• Plotting potential energy vs position gives potential energy curves that visualize interactions and dynamics.
• Potential energy is a useful tool for analyzing systems across many scientific fields.

Overall, the potential energy framework provides a powerful way to conceptualize the invisible stored energy within a system. By tracking this energy we gain deep insights into the driving forces behind motion and change. Potential energy is a foundational concept in physics and allows both qualitative and quantitative analysis of diverse systems. The ability to mathematically formulate potential energies is key to predicting and controlling the behavior of our physical world.