What Is The Kinetic And Potential Energy In A Spring?

A spring is an elastic object that stores mechanical energy. When a spring is compressed or stretched from its equilibrium position, it gains potential energy. The energy stored in a compressed or extended spring is referred to as elastic potential energy. This energy comes from the work done to stretch or compress the spring from its relaxed length. The spring contains this potential energy until it is released and allowed to return to its original shape.

Kinetic energy is the energy of motion. A moving object has kinetic energy equal to the work required to accelerate it to that speed. In the case of a spring, when the spring is released after being compressed or extended, the stored potential energy is converted into kinetic energy as the spring moves. The spring will oscillate back and forth, converting between kinetic energy and potential energy, until all the energy is dissipated through friction. The kinetic energy of the spring depends on the mass of the object attached to it and the speed of the motion.

The potential energy stored in the deformation of a spring and the kinetic energy of the resulting motion have an inverse relationship. As the spring is compressed or stretched further from its equilibrium point, more potential energy is stored. When released, this potential energy converts into kinetic energy, reaching a maximum at the equilibrium position. As the spring passes through the equilibrium point, the kinetic energy begins decreasing as potential energy builds up again in the opposite direction. This transfer between potential and kinetic energy continues as the spring oscillates until there is no more energy left in the system.

Table of Contents

Potential Energy Formula

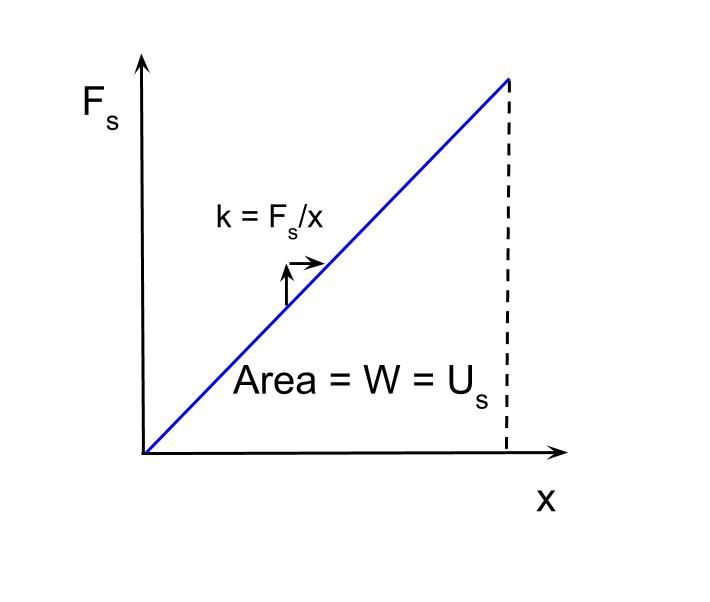
The potential energy stored in a spring depends on two factors – the spring constant (k) and the displacement (x) of the spring from its rest position. The potential energy can be calculated using the following formula:

PE = 1/2 kx²

Where:

PE is the potential energy in joules (J)
k is the spring constant in newtons per meter (N/m)
x is the displacement of the spring from its rest position in meters (m)

The spring constant (k) depends on the stiffness of the spring and measures how much force is required to compress or extend the spring. The displacement (x) is a measure of how far the spring is stretched or compressed from its natural unloaded length.

As the formula shows, the potential energy increases exponentially with displacement, because the displacement is squared. This means that stretching a spring twice as far requires four times as much energy. The potential energy is also directly proportional to the spring constant – stiffer springs require more energy to deform.

Factors affecting potential energy

The potential energy stored in a spring is determined by three key factors: the spring constant, displacement, and initial length. The potential energy can be calculated using the formula:

PE = 1⁄2 kx2

Where:

PE is the potential energy in joules (J)
k is the spring constant in newtons per meter (N/m)
x is the displacement from the equilibrium position in meters (m)

The spring constant (k) depends on the stiffness and elasticity of the spring material. A stiffer spring has a higher spring constant and stores more potential energy when compressed or stretched by a given distance. The spring constant is fixed based on the spring’s design and material.

The displacement (x) refers to how much the spring is compressed or stretched from its equilibrium length. More displacement means more potential energy stored in the spring. Displacement directly affects the potential energy in a quadratic relationship.

The initial unstretched length of the spring determines the equilibrium position. Starting from a longer initial length will increase the maximum potential energy that can be stored for a given spring constant and maximum displacement.

By understanding how these three factors affect the potential energy formula, you can calculate how much potential energy will be stored in a spring under various conditions.

Kinetic Energy Formula

The kinetic energy of a spring is the energy associated with its motion. It depends on two factors:

The mass (m) of the object attached to the spring

The speed (v) of the motion

The kinetic energy can be calculated using the following formula:

Kinetic Energy = 1/2 x m x v²

Where:

m = mass (in kg)
v = speed (in m/s)

To understand this formula, think about a spring attached to a block. When you compress or stretch the spring, you do work to give it potential energy. When released, this potential energy is converted into kinetic energy as the block starts moving.

The kinetic energy depends on the mass of the block – a more massive block will have greater kinetic energy at the same speed. Kinetic energy also depends on the square of the speed – if you double the speed, the kinetic energy increases by a factor of 4.

So in summary, the kinetic energy formula shows us that the energy of motion depends on both the object’s mass and the square of its velocity.

Relationship between kinetic and potential energy

When a spring is compressed or stretched, the energy is stored in the spring as potential energy. As the spring is released, this potential energy is converted into kinetic energy, causing the spring to start moving. The kinetic energy gives the spring the ability to do work as it expands or contracts back to its normal length.

There is a continuous transfer between potential and kinetic energy in a spring system. When the spring is at maximum compression or stretch, all the energy is potential as there is no motion. As the spring starts to expand or contract, this potential energy gets converted into kinetic energy. At the equilibrium position, when the spring is at its normal length, all the energy is kinetic and the spring is moving at maximum velocity. As the spring continues to move, the kinetic energy gets transferred back into potential energy until the spring reaches maximum compression or stretch again.

This oscillation between potential and kinetic energy continues until all the energy is dissipated due to friction, air resistance, or other losses in the system. The total mechanical energy (potential + kinetic) stays constant if we ignore these dissipative forces. This concept of energy conversion helps explain how springs and other oscillatory systems work.

Real-world examples

Springs are found in many everyday objects and provide a great way to observe the conversion between potential and kinetic energy. Here are some examples:

Slinkies – When a slinky is stretched out, it stores potential energy. When released, the coils contract and the potential energy is converted into kinetic energy, causing the slinky to bounce up and down.

Trampolines – The springs in a trampoline allow it to store potential energy when you jump on it. As you bounce, the springs first compress to store energy, then release it to launch you back upwards. The energy transforms between potential and kinetic with each bounce.

Pogo sticks – Much like a trampoline, a pogo stick contains a spring that lets you store potential energy by compressing it when you jump. This potential energy can then be released as kinetic energy to propel you upwards.

Mousetraps – The spring inside a mousetrap is initially compressed to store potential energy. When released, it converts this to kinetic energy to snap the bar shut rapidly.

Springs in cars and mattresses – Suspension springs in cars allow potential energy to be stored when they compress over bumps. This dampens the kinetic energy to produce a smoother ride. Mattress springs work similarly, compressing to absorb kinetic energy when you lie down.

Energy conservation

In an ideal spring that is not subject to friction or other non-conservative forces, the total mechanical energy of the system remains constant over time. This is known as the conservation of energy principle. The total mechanical energy is the sum of the potential energy and kinetic energy.

As a spring is stretched or compressed, it stores more potential energy. When it is released, this potential energy is converted into kinetic energy as the spring moves. The kinetic energy reaches a maximum when the spring is at its equilibrium, unstretched position. As it continues moving, the kinetic energy is converted back into potential energy until the spring reaches maximum compression or stretching again.

Throughout the cyclic motion, energy is transferred back and forth between potential and kinetic, but the total amount of mechanical energy remains the same. No energy is lost or gained, demonstrating the conservation of mechanical energy in ideal springs.

Energy dissipation

In real-world scenarios, springs do not conserve energy perfectly from kinetic to potential and back again. Some mechanical energy is dissipated or lost, usually in the form of heat and sound.

When a spring compresses or extends, the coils rub against each other producing friction. This friction results in some of the mechanical energy being converted into heat. The amount of heat produced depends on the spring material and construction. For example, steel springs tend to generate more heat than plastic springs.

The vibrations in the spring also produce sound waves in the air. These sound waves carry away some of the initial mechanical energy of the spring. The amount of energy converted to sound depends on factors like the strength of the vibrations and the density of the surrounding medium.

Springs made from elastic materials like rubber also experience energy dissipation from the stretching and reforming of polymer chains within the material. This internal friction converts mechanical energy into microscopic heat.

While the energy dissipated is usually small compared to the total energy, it does mean that the kinetic and potential energies in a given spring are not perfectly conserved. Some energy is unavoidably lost as heat and sound over time.

Summary

In summary, springs demonstrate both kinetic energy and potential energy. The potential energy stored in a spring depends on the spring constant k and how much the spring is stretched or compressed away from its relaxed length. The kinetic energy of a spring depends on its mass and velocity. As a spring oscillates back and forth, the energy transforms between potential and kinetic, with some energy dissipated as heat due to friction. The total mechanical energy remains constant in an ideal spring system without friction. Real-world springs demonstrate how kinetic and potential energy can interchange while obeying the law of conservation of energy.