What Is The Formula For Electrical Kinetic Energy?
Electrical kinetic energy is the energy that is produced by the motion of electrically charged particles. It is an important concept in electrical engineering and physics. The formula for electrical kinetic energy provides a mathematical relationship between several key variables related to electricity and motion.
The formula is: Ek = 1/2 CV2
Where Ek is electrical kinetic energy, C is capacitance, and V is voltage. This simple formula allows us to calculate the kinetic energy in a system where electric charges are moving and doing work. Understanding this formula is key for analyzing electrical systems and devices.
In this article, we will derive the full formula step-by-step starting from the basic principles of electricity and motion. We will also look at examples and applications of the formula across different electrical engineering systems and contexts.
Deriving the Formula
The formula for electrical kinetic energy can be derived from first principles using some key concepts from physics. We will start with the definition of charge.
Charge (q) is the fundamental property of matter that causes it to experience a force when placed in an electromagnetic field. Charge comes in discrete packets and can be either positive or negative. The SI unit for charge is the coulomb (C).
When charge is placed in an electric field, it experiences a force. The electric field strength (E) represents how strongly the electric field influences charged objects at a given point. It is measured in volts per meter (V/m).
Voltage (V) is the amount of potential energy between two points in a circuit. One point has more electric potential energy than the other. Voltage is what causes charges to flow in a circuit.
Capacitance (C) is the ability of a system to store an electric charge. Capacitors have capacitance and can store energy in the form of an electric field.
In physics, work (W) is done when a force (F) causes displacement (d) of an object. The work is equal to the force multiplied by the displacement.
Using all these concepts, we can now derive the formula for electrical kinetic energy.
Charge
Electric charge is a fundamental property of matter that exists in two types – positive and negative. Charge is measured in coulombs (C), named after French physicist Charles-Augustin de Coulomb. The amount of charge an object has determines the strength of its electrical interactions with other charged objects. For example, electrons have a negative charge, while protons have a positive charge.
Charge plays a key role in electrical kinetic energy. Objects that have electric charge also have an electric field associated with them. When charges move relative to their electric field, they gain kinetic energy that is quantified by the object’s charge, the strength of the electric field, and the displacement or distance traveled. Greater electric charge and electric field strength, as well as greater displacement, leads to greater electrical kinetic energy. Therefore, the amount of charge is directly proportional to the kinetic energy an object gains when moving through an electric field. This relationship is a key part of the formula for electrical kinetic energy.
Electric Field
An electric field is created by electric charges. It describes the amount of force experienced by another electric charge placed into the field. Electric charges generate an electric field around them. The strength of the electric field depends on the amount of charge and decreases in proportion to the square of the distance from the charge.
The electric field strength is measured in units of newtons per coulomb (N/C) or volts per meter (V/m). One volt per meter is equivalent to one newton per coulomb. The electric field strength quantifies the amount of force exerted on a test charge by the electric field at a given point. A greater electric field strength indicates a stronger force on the test charge. The direction of the electric field at a point matches the direction of the force exerted on a positive test charge.
The electric field strength is directly proportional to the voltage at a given point. Voltage represents the amount of potential energy per unit charge at a location in the electric field. Therefore, a higher voltage corresponds to a stronger electric field that can exert more force on charges. The relationship between voltage and electric field allows us to calculate one quantity based on the other.
Voltage
Voltage, also called electric potential difference, is the difference in electric potential between two points. It measures the “push” or “pressure” of electricity. Voltage is measured in volts and represented by the symbol V.
Imagine electricity is like water flowing through pipes. The voltage is like the water pressure – it’s what pushes the electrons to flow through a wire, similar to how water pressure pushes water through pipes. Places with higher voltage have more “pressure” pushing electrons.
Voltage causes electric current to flow in a circuit. The higher the voltage, the more current will flow for a given resistance. Devices like light bulbs are given a rated voltage that provides the optimal current flow for their safe operation.
In summary, voltage represents the potential for current to flow in an electrical circuit. It provides the “push” needed for electric charges to move. The volt unit measures this electric potential difference between two points in a circuit.
Capacitance
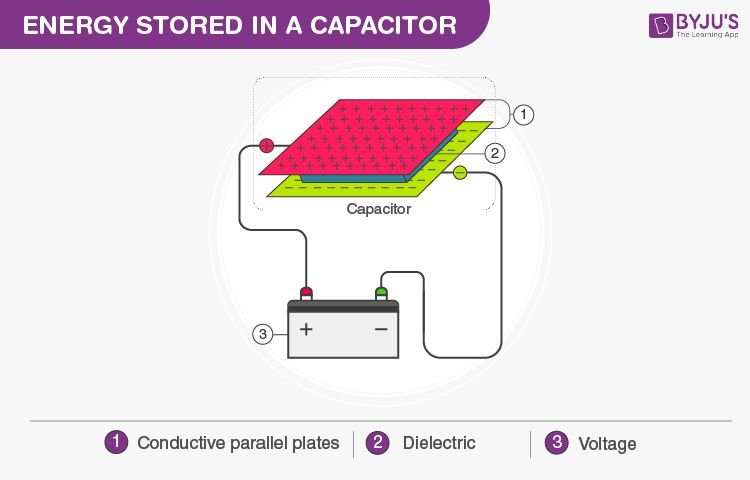
Capacitance is the ability of a body to store an electric charge. It is related to electrical kinetic energy because capacitors store energy in the form of an electric field. Capacitance depends on the geometry of the conductors, the distance between them, and the permittivity of the dielectric material between the conductors. Capacitance is measured in farads, named after physicist Michael Faraday. A farad is defined as one coulomb of charge stored per volt of electric potential difference. Most capacitors have capacitances in the microfarad (μF) or picofarad (pF) range.
When a voltage is applied across a capacitor, electrons accumulate on one plate and depart from the other plate, resulting in separated positive and negative charges. This separation of charge creates an electric field that stores energy. The capacitance determines how much charge can be stored for a given voltage. A larger capacitance allows more charge to be stored. The energy stored in a capacitor is proportional to the capacitance and to the square of the voltage. Thus, capacitance is a key factor relating to the energy storage capacity of a capacitor.
Work, Force, Displacement
To understand how electrical kinetic energy is derived, we first need to review some basic concepts from physics. Specifically, the relationships between work, force and displacement.
Work is defined as force applied over a distance. In equations, this is written as:
Work = Force x Displacement
Or:
W = Fd
Where W is work, F is force, and d is displacement.
Displacement refers to the change in position of an object. So if an object moves 5 meters to the right, its displacement is 5 meters.
Force is defined as anything that can cause an object to accelerate. It is measured in Newtons.
So in plain terms, work occurs when a force causes an object to move. The amount of work done depends on the amount of force applied and the distance the object moves.
These concepts are key to understanding how electrical kinetic energy is derived, as we’ll see shortly.
The Formula
The formula for electrical kinetic energy is:
Ek = 1/2 CV2
Where:
Ek = Electrical kinetic energy (in joules)
C = Capacitance (in farads)
V = Voltage (in volts)
This formula shows that the electrical kinetic energy stored in a capacitor is equal to one-half the capacitance multiplied by the square of the voltage. Intuitively, this makes sense because capacitance determines how much charge can be stored, while voltage determines the potential energy per unit charge. Squaring the voltage gives us the total energy. The 1/2 factor comes from deriving the formula based on integrating the incremental work done in building up charge on a capacitor.
Examples
Here are some examples calculating electrical kinetic energy using the formula:
Example 1:
Let’s say a capacitor with a capacitance of 5 farads is charged up to a voltage of 12 volts. What is the electrical kinetic energy stored in the capacitor?
Plugging the values into the formula:
KE = (1/2)CV2
= (1/2)(5 farads)(12 volts)2
= 360 joules
So the kinetic energy stored is 360 joules.
Example 2:
An electric field of 3000 N/C exerts a force on an electron with a charge of -1.6 x 10-19 C, moving it a distance of 0.5 meters. What is the electrical kinetic energy?
First, calculate the work done:
W = Fd
= (3000 N/C)(-1.6 x 10-19 C)(0.5 m)
= -2.4 x 10-16 J
Then the kinetic energy is:
KE = W
= -2.4 x 10-16 J
So in this example, the kinetic energy is -2.4 x 10-16 joules.
Applications
The formula for electrical kinetic energy has many important real-world applications, especially in electrical engineering and electronics.
One of the most common applications is in capacitors. Capacitors store electrical energy by accumulating electric charge on two conductors separated by an insulator. When a capacitor is connected to a voltage source like a battery, charge flows onto the plates, storing energy in the electric field between the plates. The amount of energy stored in a capacitor is directly calculated from the formula for electrical kinetic energy.
Batteries also rely on the same formula to determine their capacity for storing and delivering electrical energy. Within a battery, chemical reactions generate charge that accumulates on the positive and negative terminals. The total electrical energy available from the battery depends on its capacitance and the voltage. Knowing the formula allows calculating a battery’s energy density and lifespan.
In electric circuits, the formula provides the basis for analyzing how much power capacitors and inductors can deliver. It determines the energy stored in electric and magnetic fields within the circuit components. This aids circuit design and optimization.
The formula is also important in consumer electronics. For example, it helps evaluate the battery life for devices like smartphones and laptops. It also assists in selecting appropriate capacitors for functions like power regulation and filtering in electronic devices.
Even in large power systems like the electrical grid, the formula for electrical kinetic energy assists in assessing the capabilities of equipment like generators and transmission lines for delivering electricity.
Understanding this fundamental relationship between charge, voltage, and capacitance provides the foundation for working with electrical energy across many different disciplines and applications.