What Is The Equation For Energy Conversion?
Energy conversion refers to the process of changing energy from one form to another. The law of conservation of energy states that energy cannot be created or destroyed, only converted from one form to another. There are many different equations used to calculate the conversion of energy from one form to another. The main types of energy conversion equations involve converting between potential energy, kinetic energy, thermal energy, electrical energy, chemical energy, nuclear energy, mechanical energy, light energy, and sound energy.
This article will provide an overview of the key equations used for converting between different forms of energy. Understanding these fundamental energy conversion equations is important across many scientific and engineering fields.
Potential Energy
Potential energy is the energy held by an object because of its position or chemical composition. There are several types of potential energy, including gravitational potential energy.
Gravitational potential energy refers to the energy stored in an object due to gravity. For example, a ball held at a height above the ground has gravitational potential energy due to the height it is held at and the gravitational pull of the Earth. The equation for gravitational potential energy is:
PEg = m x g x h
Where:
PEg is the gravitational potential energy
m is the mass of the object
g is the acceleration due to gravity (9.8 m/s2 on Earth)
h is the height of the object above a reference point
This equation shows that an object’s gravitational potential energy increases linearly with height for a given mass and gravitational acceleration. The reference point is often set to zero, so the height h represents the vertical distance above that point. This equation allows calculation of gravitational potential energy changes as an object moves in a gravitational field.
Kinetic Energy
Kinetic energy is the energy associated with motion. An object that has motion, either translational or rotational, has kinetic energy. The amount of kinetic energy an object has depends on its mass and velocity. The faster an object moves, the more kinetic energy it has. Heavier objects also have more kinetic energy at the same velocity than lighter objects.
Kinetic energy can be described by the following equation:
Ek = 1/2 mv2
Where:
- Ek is kinetic energy in joules (J)
- m is mass in kilograms (kg)
- v is velocity in meters per second (m/s)
This is known as the kinetic energy equation. It shows that kinetic energy is directly proportional to both mass and the square of velocity. So by increasing either mass or velocity, the kinetic energy will increase exponentially.
Kinetic energy is a form of mechanical energy associated with motion. Some common examples include a ball in flight, a car driving, or an airplane in flight. The kinetic energy equation allows this energy to be quantified.
Thermal Energy
Thermal energy refers to the internal energy present in substances due to the kinetic motion and potential energy of the molecules and atoms. It is directly proportional to the temperature of the substance. Thermal energy can be transferred between substances through heat transfer. The main mechanisms of heat transfer are conduction, convection and radiation.
The rate of conductive heat transfer is given by Fourier’s law:
q = -kA(dT/dx)
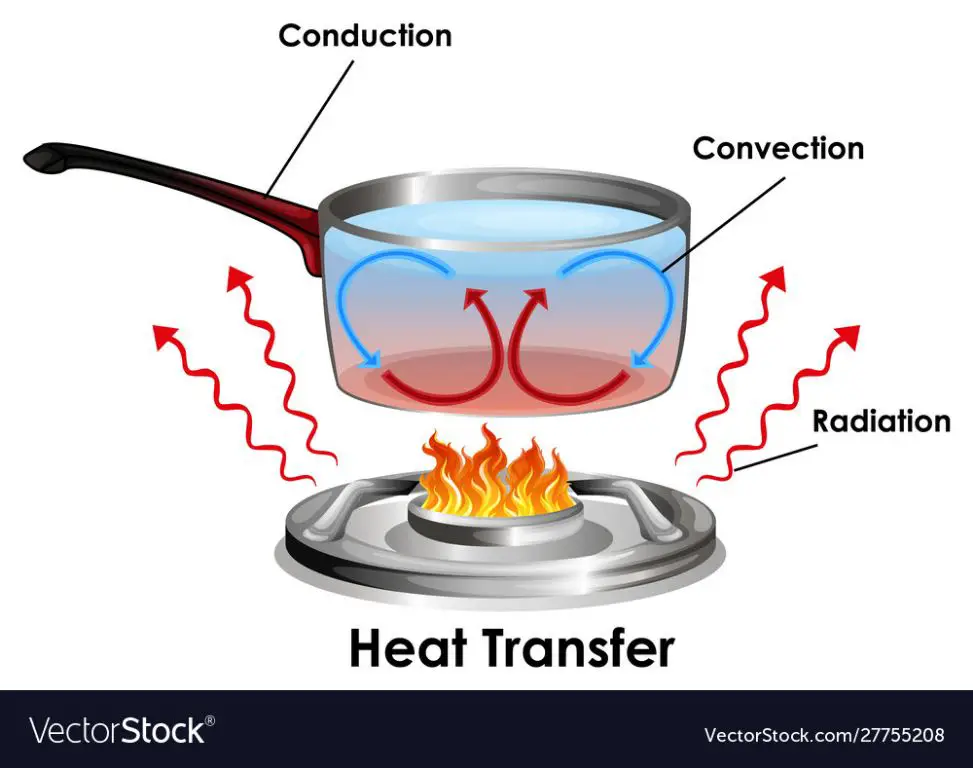
Where q is the heat transfer rate, k is the thermal conductivity, A is the cross-sectional area, and dT/dx is the temperature gradient. This equation shows that heat transfer is proportional to the temperature gradient and cross-sectional area.
Convective heat transfer involves the bulk motion of fluids and is described by Newton’s law of cooling:
q = hA(Ts – T∞)
Where h is the convective heat transfer coefficient, A is the surface area, Ts is the surface temperature, and T∞ is the fluid temperature. This equation shows convective heat transfer is proportional to the temperature difference.
In thermodynamics, the First Law states that energy is conserved. For a closed system undergoing a process, this is mathematically stated as:
ΔEsystem = Q – W
Where ΔEsystem is the change in the system’s internal energy, Q is the heat transfer into the system, and W is the work done by the system. This first law equation is the basis for analyzing energy transfers involving thermal energy.
Electrical Energy
Electrical energy is the energy derived from the movement of electrons. It is one of the most widely used and versatile forms of energy in modern society. Electrical energy powers everything from lightbulbs to computers to industrial machinery.
The basic equation for electrical power is:
Power (P) = Current (I) x Voltage (V)
Where power is measured in Watts, current is measured in Amps, and voltage is measured in Volts. This shows that power increases as either current or voltage increases.
Other key electrical energy equations:
Power (P) = Energy (E) / Time (t)
Energy (E) = Power (P) x Time (t)
These equations show the relationship between power, energy, and time. Energy is power exerted over time. The greater the power or time, the greater the energy.
Electrical energy is extremely useful because it is easily converted into other forms of energy like heat, light, and motion. However, transmitting and storing electrical energy can be challenging. The electrical grid was developed specifically for widespread transmission and distribution of electricity.
Chemical Energy
Chemical energy is the potential energy stored in the bonds between atoms and molecules. Chemical energy can be converted into other forms of energy when chemical bonds are formed or broken. Some key chemical energy equations include:
Combustion reactions – Chemical energy is converted into thermal energy and light when fuels like gasoline, natural gas or wood are burned. The chemical reaction is:
Fuel + Oxygen → Carbon Dioxide + Water + Heat + Light
Batteries – Chemical energy is converted into electrical energy in batteries. The chemical reactions involve the movement of electrons which generates an electric current. For example, in a zinc-copper voltaic cell:
Zn(s) + Cu2+ (aq) → Zn2+ (aq) + Cu(s)
Digestion – The breakdown of large food molecules like carbohydrates, proteins and fats releases chemical energy that cells use for growth and function. The overall chemical reaction is:
Food molecules + Oxygen → Carbon Dioxide + Water + Energy
Photosynthesis – Plants convert light energy from the sun into chemical energy stored in glucose and other organic compounds. The chemical reaction is:
6CO2 + 6H2O + Light → C6H12O6 + 6O2
In summary, chemical energy involves the making and breaking of atomic bonds during chemical reactions. This energy can be released as heat, light or electricity for practical use.
Nuclear Energy
Nuclear energy comes from the splitting of atoms in a process called nuclear fission or the fusing of atoms in a process called nuclear fusion. In both fission and fusion, mass is converted into energy according to Einstein’s equation:
E = mc2
Where E is energy, m is mass, and c is the speed of light.
In nuclear fission, a heavy radioactive element like uranium or plutonium splits into two lighter nuclei, releasing energy in the process. The fission of 1 gram of uranium-235, for example, produces about 20 trillion joules of energy.
In nuclear fusion, two light atomic nuclei fuse together to form a heavier nucleus, also releasing energy. Fusion of 1 gram of deuterium, a hydrogen isotope, with 1 gram of tritium, another hydrogen isotope, produces about 94 trillion joules of energy.
Nuclear power plants use fission reactions to heat water and produce steam that spins turbines to generate electricity. Fusion reactions are not yet used to generate power but are the focus of intensive research to develop fusion power in the future.
Mechanical Energy
Mechanical energy is the energy associated with the motion and position of an object. It is the sum of an object’s kinetic energy and potential energy. Mechanical energy can be transferred between objects through work.
The work-energy theorem states that the net work (W) done on an object equals its change in kinetic energy (ΔKE). This is represented by the equation:
W = ΔKE
Work is done when a force (F) acts on an object and the object moves through a distance (d). The work done equals the force multiplied by the distance.
W = F x d
Since W = ΔKE, we can set the two equations equal to each other:
F x d = ΔKE
This shows that when a net force acts on an object over a distance, the object’s kinetic energy changes. The work-energy theorem is important for analyzing mechanical systems and how energy transfers between objects through work.
Light Energy
Light energy is a form of radiant energy that is created by electromagnetic waves. The solar energy from the Sun that reaches Earth is the most common example of light energy. When sunlight hits an object, the energy can be reflected, absorbed, or pass through the object.
Light energy is a type of kinetic energy because it involves photons in motion. Photons are the smallest units of light energy. They have no mass but carry momentum. The energy of a photon, called photon energy, is directly proportional to its frequency and inversely proportional to its wavelength. This relationship is described by the Planck–Einstein equation:
E = hf
Where E is the photon energy, h is Planck’s constant, and f is the frequency of the photon. This equation shows that higher frequency photons have higher energy.
Photon energy follows the electromagnetic spectrum, with radio waves having low frequency/energy and gamma rays having high frequency/energy. Visible light that humans can see falls in the middle of the spectrum. When a photon is absorbed by an atom or molecule, its energy can be transferred to excite an electron to a higher energy state. This is how light energy from the Sun is captured through photosynthesis to power life on Earth.
Sound Energy
Sound energy is the energy carried by sound waves. Sound waves are longitudinal mechanical waves that propagate through gases, liquids, and solid materials. These waves are generated by the vibration of an object, which causes molecules in the surrounding medium to vibrate. This vibration creates alternating bands of compression and rarefaction that transmit energy through the medium.
The intensity of sound energy is related to the amplitude of the sound wave. Greater amplitude means more energy is carried by the wave. The loudness of a sound perceived by the human ear depends on both the intensity of the sound wave and the frequency. Higher frequency sounds are perceived as louder for a given intensity.
The basic equation that relates the energy carried by a sound wave to its physical characteristics is:
Sound energy = Amplitude2 x Frequency
Where amplitude is the maximum displacement of molecules in the wave, and frequency is the number of cycles per second. This equation shows that energy is proportional to the square of the amplitude, so doubling the amplitude quadruples the energy. It also shows that higher frequency waves carry more energy for the same amplitude.
Other important equations used in acoustics and sound wave physics include:
Speed of sound = Wavelength x Frequency
This relates the speed of propagation to the wavelength and frequency.
Intensity = Power / Area
This calculates the intensity or power delivered per unit area by a sound wave. Combining this with the first equation gives the full relationship between sound wave power, intensity, amplitude and frequency.