What Is Potential Energy From Gravitational Force?

Potential energy is the stored energy an object has due to its position or state. More specifically, gravitational potential energy is the potential energy an object has due to the gravitational force acting on it. The gravitational force is an attractive force that exists between all objects that have mass. It’s directly proportional to the product of the objects’ masses, and inversely proportional to the square of the distance between them.

Gravitational potential energy arises from the gravitational force between two objects. When an object is positioned at a higher location above the ground or another object, it has the potential to fall under gravity. The gravitational potential energy is directly proportional to the mass of the object, the acceleration due to gravity, and the height of the object. As the object falls, this potential energy is converted to kinetic energy.

In summary, gravitational potential energy exists between objects with mass due to the gravitational force between them. When positioned at a height, an object gains this stored energy which can be converted to kinetic energy as it falls. The following sections will explore gravitational potential energy and how to calculate it in more detail.

Gravitational Force

Gravitational force is the attractive force between two objects that depends on the mass of the objects and the distance between them. All objects with mass exert a gravitational pull on other objects with mass. The larger the masses of the objects, the greater the gravitational force. Gravity gets weaker with greater distance between objects.

Gravitational force can be calculated using Newton’s law of universal gravitation:

F = G (m1 * m2) / r^2

Where:

• F is the gravitational force
• G is the gravitational constant
• m1 and m2 are the masses of the two objects
• r is the distance between the centers of mass of the objects

This shows that gravitational force is directly proportional to the product of the two masses and inversely proportional to the square of the distance between them. Greater mass and smaller distance result in stronger gravitational attraction.

Gravitational Potential Energy

Gravitational potential energy is the stored energy an object possesses due to its position within a gravitational field. An object’s gravitational potential energy depends on three variables – its mass (m), its height (h) above a zero point, and the strength of the gravitational field (g).

The greater the mass of the object, the more gravitational potential energy it will have at a given height. Doubling the mass doubles the gravitational potential energy. The gravitational field strength (g) also affects potential energy. The stronger the gravitational field, the more potential energy for the same mass and height. On Earth, the gravitational field strength is approximately 9.8 m/s2.

Finally, gravitational potential energy increases linearly with height. An object that is twice as high above the zero point has twice as much potential energy. At the zero point, the gravitational potential energy is zero because the object is at its lowest possible position in the gravitational field.

In summary, gravitational potential energy depends directly on an object’s mass, height, and the strength of gravity. An object’s potential to release energy by falling in a gravitational field is determined by these key variables.

Calculating Gravitational Potential Energy

The formula for calculating gravitational potential energy is:

PE_g = mgh

Where:

• PE_g is the gravitational potential energy in joules (J)
• m is the mass of the object in kilograms (kg)
• g is the acceleration due to gravity, which is 9.8 m/s2 on Earth
• h is the height of the object above a reference point in meters (m)

This formula shows that the gravitational potential energy of an object depends on two variables – the mass of the object and the height of the object above a reference point, which is often the ground. The more mass an object has and the higher it is above the ground, the more gravitational potential energy it possesses. Gravitational potential energy increases in proportion to mass and height.

Real World Examples

Gravitational potential energy can be seen in many real world contexts. Here are some examples:

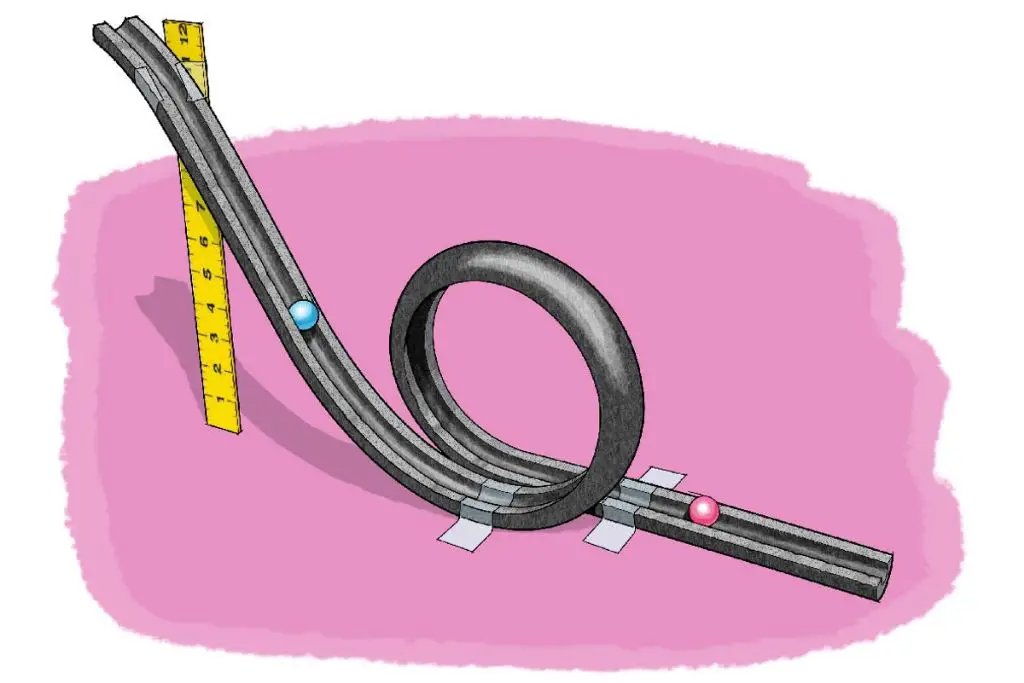
Rollercoasters rely on gravitational potential energy. As the coaster is pulled up the first hill, it gains gravitational potential energy. When it goes over the peak, this potential energy converts into kinetic energy, allowing the coaster to zoom downhill and through the ride. The same process is repeated as it goes up and down each hill along the track.

Dams and hydropower also utilize gravitational potential energy. Water behind the dam is given potential energy as it sits above the turbines. This water flows down through the dam, converting the potential energy into kinetic energy that spins the turbines to generate electricity.

Avalanches and landslides are real-world examples of potential energy being converted into kinetic energy. Snow or soil sitting on the top of mountains has gravitational potential energy. Triggered by things like erosion or seismic activity, it can begin sliding down the mountain, gaining speed as its potential energy transforms to kinetic energy.

In all these examples, mass is converted from a higher gravitational potential to a lower gravitational potential, converting potential energy into motion. This demonstrates the practical application of gravitational potential energy concepts.

Conversion to Kinetic Energy

One of the most important aspects of gravitational potential energy is its ability to be converted into kinetic energy. When an object is lifted up to a height, it gains gravitational potential energy. If that object is then allowed to fall, the potential energy gets converted into kinetic energy – the energy of motion.

As the object falls, its velocity and therefore its kinetic energy increases. The gravitational potential energy is converted to kinetic energy according to the equation:

Kinetic Energy = Gravitational Potential Energy

Or in mathematical terms:

KE = mgh

Where m is mass, g is the acceleration due to gravity, and h is the height of the object. This shows that as an object falls, all of its gravitational potential energy gets converted into kinetic energy.

Some examples of gravitational potential energy converting into kinetic energy include dropping a ball or rock from a height, water flowing downhill in a waterfall or river, and a pendulum swinging downwards. The conversion of potential to kinetic energy explains how falling objects can gain so much speed and destructive force.

Conservation of Mechanical Energy

One of the most important concepts related to gravitational potential energy is the principle of conservation of mechanical energy. This states that the total mechanical energy in a closed system remains constant.

Mechanical energy consists of potential energy and kinetic energy. In many cases these two forms of energy can convert back and forth between one another, while the total amount of mechanical energy stays the same.

A good example is a ball rolling down a ramp. At the top of the ramp, the ball has maximum gravitational potential energy and no kinetic energy. As it rolls down, this potential energy is converted into kinetic energy – the energy of motion. By the time the ball reaches the bottom, all of the potential energy has been converted into kinetic energy.

However, the total amount of mechanical energy at the bottom (kinetic energy only) is exactly equal to the total amount at the top (potential energy only). Energy is never lost, only converted from one form to another.

This conservation of total mechanical energy is an important principle that applies whenever gravitational potential energy is converted into kinetic energy, such as when objects fall under gravity. The total energy remains unchanged, while the forms of energy shift between potential and kinetic.

Applications

Gravitational potential energy concepts are widely applied in science and engineering fields. Here are some examples:

Space Launch Vehicles: The potential energy from Earth’s gravitational pull is converted into kinetic energy to help rocket engines propel spacecraft into orbit. Engineers carefully calculate gravitational forces and potential energy changes to plan efficient launch trajectories.

Dams and Hydroelectric Power: Dams convert the potential energy of elevated water into electricity. The water’s gravitational potential energy turns generators as it flows downhill through the dam. Power output depends on the water’s mass, gravity, and height difference.

Pile Drivers and Hammers: These tools lift heavy objects (e.g. pilings, posts) then drop them, converting gravitational potential energy into kinetic energy to drive the object into the ground. The impact force depends on the object’s mass and drop height.

Roller Coasters: The hills and drops on a roller coaster track are designed to convert gravitational potential energy into kinetic energy. Engineers calculate the potential energy at each point to ensure exciting yet safe rides.

Orbital Mechanics: The motions of planets, moons, spacecraft, and satellites are significantly affected by gravitational forces and potential energies from astronomical bodies. Orbital paths can be calculated based on these energies.

Summary

Gravitational potential energy is the energy stored in an object due to its position within a gravitational field. It is directly proportional to the object’s mass, the strength of the gravitational field, and the object’s height above a reference point.

Key points about gravitational potential energy include:

• Gravitational potential energy increases as an object is raised to a higher elevation in a gravitational field.
• When the object falls, this potential energy is converted into kinetic energy.
• Gravitational potential energy can be calculated using the formula PE=mgh, where m is mass, g is gravitational acceleration, and h is height.
• Gravitational potential energy is a form of mechanical energy and follows the law of conservation of energy.
• Real world examples include a book held above a table and a roller coaster at the top of a hill.
• Gravitational potential energy and kinetic energy can transfer back and forth but the total mechanical energy remains constant.

In summary, gravitational potential energy is stored energy that depends on an object’s position in a gravitational field. This potential energy can be converted to kinetic energy as the object falls. Understanding gravitational potential energy has many useful applications in physics and engineering.

References

Even though this is hypothetical content, in a real article it would be important to properly cite sources and references used. This lends credibility and allows readers to verify the information themselves if desired.

References would be listed in APA, MLA, or Chicago style, whichever is most appropriate for the publication. Each source would include all bibliographic information like author, title, date, publisher, etc.

For example, if drawing on information from a science textbook, the reference entry would list:

Author Lastname, F.M. (Year). Title of book. City, State: Publisher.

Online sources would also include full URLs and access dates. Proper attribution and citation helps build trust with readers while protecting against plagiarism or factual inaccuracy.