What Factors Affect The Energy In A Kinetic Energy Store?

Definition of Kinetic Energy

Kinetic energy is the energy of motion. It is defined as the work needed to accelerate a body of a given mass from rest to its stated velocity. Having gained this energy during acceleration, the body keeps this kinetic energy unless its speed changes. The same amount of work is done by the body when decelerating from its current speed to a state of rest.

In classical mechanics, the kinetic energy of a non-rotating object of mass m traveling at a speed v is one half mv2. In SI units, these quantities are measured in kilograms, meters per second squared, and joules.

For example, a 5 kg object moving at 10 m/s has a kinetic energy of 250 joules. This is calculated by 0.5 x 5 x (10 x 10) = 250 joules. If the object were to double its speed to 20 m/s, its kinetic energy would increase to 1000 joules.

Equation for Kinetic Energy

The equation for kinetic energy is 1/2mv^2, where:

• m is the mass of the object in kilograms (kg)
• v is the velocity of the object in meters per second (m/s)

Kinetic energy depends on both the mass and the velocity of an object. For a given mass, the kinetic energy will increase exponentially as the velocity increases. This is due to the velocity term being squared in the equation.

Mass

The mass of an object directly impacts its kinetic energy. Kinetic energy depends on the mass (m) of the object, as shown in the kinetic energy equation:

Kinetic Energy = 1/2 * m * v²

Where m is mass and v is velocity. According to the equation, an increase in mass will lead to a proportional increase in kinetic energy, assuming velocity is held constant. This is because a more massive object moving at the same speed as a less massive object has more inertia. Greater inertia means it takes more work or energy to get the object moving. An object with more mass concentrates the same amount of energy into a smaller space, resulting in greater kinetic energy. This is why a moving truck has much higher kinetic energy than a moving bicycle, even if both are traveling at the same velocity. In summary, the greater the mass of an object, the greater its kinetic energy will be.

Velocity

Velocity, or speed, is a key factor that affects the amount of kinetic energy in an object. The faster an object is moving, the greater its kinetic energy. This is because kinetic energy is directly proportional to the square of an object’s velocity, as shown in the kinetic energy equation:

KE = 1/2 mv^2

Where m is mass and v is velocity. This quadratic relationship means that if velocity is doubled, kinetic energy increases by a factor of 4. Small increases in velocity can result in large increases in kinetic energy.

For example, a car traveling at 100 km/hr has 4 times the kinetic energy of a car traveling at 50 km/hr. This is why high velocity impacts or collisions can be extremely destructive – even small increments in velocity can exponentially increase the kinetic energy.

In summary, velocity is a critical factor affecting kinetic energy. The faster an object moves, the greater its kinetic energy will be. This is why controlling velocity is important for limiting kinetic energy in contexts like transportation and industrial machinery.

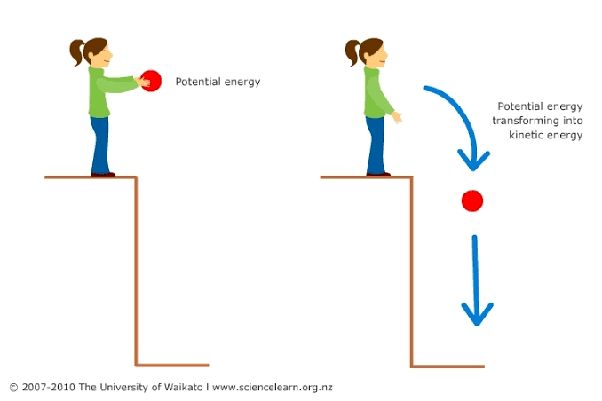
Height

The height of an object directly impacts the amount of potential energy it possesses, which can be converted into kinetic energy. Potential energy is the stored energy an object has due to its position or state. The higher up an object is relative to the ground or a zero height position, the greater its potential energy will be due to the influence of gravity. Gravity will cause an object at rest at a height to accelerate downward, converting this potential energy into kinetic energy, which is the energy of motion.

For example, consider a ball held at the top of a building versus on the ground. The ball at the top of the building is at a greater height above the ground, so it has more potential energy stored. If released, gravity will accelerate the ball downward, converting that potential energy into kinetic energy and increasing its speed. The ball on the ground has no height, so limited potential energy to convert into kinetic energy. Therefore, the greater the height of an object, the more potential energy it can convert into kinetic energy if allowed to drop.

Friction

Friction is a force that opposes the motion of an object, resulting in a loss of kinetic energy. When two surfaces rub against each other, friction converts some of the kinetic energy into thermal energy in the form of heat. The kinetic energy of a moving object is proportional to its mass and the square of its velocity. Friction reduces the velocity, so the kinetic energy decreases rapidly. The rougher the surfaces in contact, the greater the friction and kinetic energy loss. Friction can never increase the kinetic energy of an object. It only takes kinetic energy away.

For example, when you slide a block of wood across a table, friction between the block and table surface slows the wood down until it stops. The kinetic energy is transformed into heat. Spinning tires losing traction on a sandy surface is another example of friction converting kinetic energy into thermal energy. The friction force between the tires and sand causes the tires to slow down and heat up. Minimizing friction is an important design goal in mechanical systems to maintain kinetic energy.

Wind Resistance

Wind resistance, or drag, is a force that opposes the motion of an object. As an object moves through the air, it has to push the air molecules out of the way. These air molecules exert a resistive force back on the object, slowing it down. The faster the object moves, the more air molecules it encounters, and the greater the wind resistance.

For objects moving through the air, like cars, planes, and projectiles, wind resistance reduces their kinetic energy over time. The kinetic energy is converted into other forms like heat and sound as the object is slowed down by dragging air molecules along with it. Without an external force like a propeller or engine providing thrust, the kinetic energy of an object will steadily decrease due to wind resistance.

The effects of wind resistance are very noticeable at high speeds. For example, skydivers reach terminal velocity after 12-15 seconds of free fall, when the wind resistance equals the gravitational force. Race cars utilize aerodynamic designs to reduce wind resistance and maintain high speeds. In sports, balls like golf balls and baseballs are designed with dimples to reduce drag. Overall, accounting for wind resistance is an important factor when examining the kinetic energy of moving objects.

Gravity

Gravity is perhaps the most significant factor that affects the kinetic energy of an object. When gravity accelerates an object downwards, it increases the object’s velocity and thus kinetic energy. According to Newton’s second law, the acceleration due to gravity on Earth is around 9.8 m/s2. This means that every second, a free falling object will increase its velocity by 9.8 m/s. The kinetic energy of an object is calculated by 1⁄2mv2, so an increase in velocity results in a disproportionate increase in kinetic energy.

For example, consider a 1kg ball that is dropped from a height of 10m. As the ball falls, its velocity increases by 9.8 m/s each second due to gravity. After 1 second the velocity is 9.8 m/s, after 2 seconds it is 19.6 m/s, and so on. Using the kinetic energy equation, the energy after 1 second is 49 J, after 2 seconds it is 196 J, and so on. This shows how the kinetic energy increases exponentially as the velocity increases due to gravity.

Gravity is always acting on objects above the Earth’s surface. When designing systems that involve moving objects, the effects of gravitational acceleration and the resulting kinetic energy must be considered. Devices such as brakes are needed to counteract gravity and reduce kinetic energy in many cases.

Acceleration

Acceleration affects kinetic energy because kinetic energy depends directly on an object’s velocity. The greater the acceleration, the more velocity increases over a given time. Acceleration is defined as the rate of change in velocity over time. Mathematically, acceleration is the first derivative of velocity with respect to time.

When an object accelerates due to the application of a force, its velocity changes in the direction of the applied force. For example, when you step on the gas pedal in a car, the engine applies a force to accelerate the car forward, increasing its velocity in the forward direction. This increase in velocity means the car’s kinetic energy increases as well. The greater the acceleration, the faster the increase in velocity and kinetic energy.

This relationship applies to any object being accelerated. A rocket launching into space, a rollercoaster speeding up as it descends, a tennis ball being served harder – greater acceleration leads to greater velocity gain and greater increase in kinetic energy. Acceleration is a key factor determining how much and how quickly kinetic energy can be transferred to an object.

Examples

Here are some examples that demonstrate how various factors can affect the kinetic energy of an object:

Falling object

As an object falls from a height, its velocity increases due to gravity. This increases its kinetic energy. The higher the initial height, the greater the final velocity and kinetic energy.

Moving vehicle

A vehicle’s kinetic energy depends on its mass and velocity. A more massive vehicle, traveling at the same speed as a lighter one, will have greater kinetic energy due to its higher mass. Increasing the vehicle’s velocity will also increase its kinetic energy.

Rolling ball

A ball rolling across a rough surface will experience friction which slows it down, reducing its kinetic energy over time. On a very smooth surface with less friction, the ball retains more of its original kinetic energy.

Pendulum swing

As a pendulum swings back and forth, its kinetic energy converts to potential energy at the top of the swing, and back to kinetic energy at the bottom. This exchange conserves the total energy of the system.