How Do You Calculate Potential Energy From Force?
Definition of Potential Energy
Potential energy is a form of stored energy that exists within an object because of its position or arrangement. It refers to the capacity of an object to do work as a result of its position or configuration.
For example, a ball at the top of a hill has potential energy because of gravity pulling it down. As the ball rolls down the hill, this potential energy gets converted into kinetic energy, or the energy of motion. The higher the ball is elevated, the greater its potential energy.
Potential energy represents stored work, waiting to be released and transformed into kinetic energy. It exists in various forms, such as gravitational potential energy, elastic potential energy, chemical potential energy, and more. Understanding the concept of potential energy is key to explaining how many systems in physics work.
Relationship Between Force and Potential Energy
Potential energy is closely linked to force. Force is defined as anything that can cause an object with mass to accelerate. It involves one object exerting a push or pull on another object. For example, lifting a book involves applying an upward force to raise it. The force applied against gravity increases the potential energy of the book.
The greater the force exerted on an object, the more potential energy it gains. This is because it takes more force to move an object against a greater opposing force. For instance, lifting a heavier book requires more force than a lighter book. The heavier book gains more potential energy due to the greater force exerted.
In summary, potential energy depends directly on the amount of force applied. More force exerted leads to greater potential energy. The relationship between force and potential energy is key to understanding how to calculate potential energy.
Calculating Potential Energy
The most important formula for calculating potential energy is:
PE = F * d
Where:
- PE is the potential energy
- F is the force applied
- d is the distance over which the force is applied
This simple formula shows the direct relationship between force, distance, and potential energy. Potential energy increases linearly with greater force or distance. Intuitively, we know it takes more “potential” to lift a heavier object a greater height, which requires more force over a longer distance.
To calculate potential energy using this formula:
- Identify the force (in Newtons) acting on the object
- Identify the distance (in meters) over which the force acts
- Multiply the force by the distance to calculate the potential energy
The potential energy will be in units of Joules, which is a derived unit equal to (Newtons * meters). This formula demonstrates the direct relationship between force, distance, and energy.
Understanding the Variables
When calculating potential energy from force, it’s important to understand the key variables involved in the equation:
F is force, measured in newtons (N). Force is a measurement of the interaction between two objects, specifically the push or pull on an object. For calculating potential energy, this is the force being exerted on the object.
d is distance, measured in meters (m). This is the distance over which the force is being exerted on the object. For potential energy, it refers to the height or vertical displacement of the object.
So in simple terms, F is the force acting on an object, and d is the distance that object is raised against that force. Understanding the meaning behind these key variables is essential for being able to correctly calculate potential energy from force.
Units of Potential Energy
When calculating potential energy, it is important to use the proper units. Potential energy is expressed in joules (J) in the SI (metric) system. The joule is the standard unit of energy in physics and defined as the work done by a force of one newton acting over a distance of one meter.
Some key facts about joules:
- 1 J = 1 kg * m^2 / s^2
- 1 J is the amount of energy to raise a 1kg object by 1 meter against gravity
- 1 J is the amount of work to move an electric charge of 1 coulomb through an electrical potential difference of 1 volt
Always make sure to express your final potential energy calculation in joules to be consistent with standard scientific convention. The joule unit enables clear communication and understanding when quantifying potential energy.
Potential Energy Examples
There are many everyday examples of potential energy that we encounter. Two common ones are lifting objects and stretching springs.
When you lift an object from the ground, you are moving it against the pull of gravity. The higher you lift it, the more potential energy it has. Specifically, the potential energy PE gained by lifting an object of mass m to height h is calculated as:
PE = mgh
Where g is the gravitational acceleration constant. This shows that the potential energy increases linearly with height for a given mass. For example, lifting a 5kg object to a height of 2m gives a potential energy of 5kg x 9.8m/s2 x 2m = 98 J.
Springs also demonstrate potential energy when they are stretched or compressed. The more a spring is displaced from its relaxed length, the more potential energy it gains. This potential energy is released as kinetic energy when the spring recoils back to its original shape. The potential energy stored in a spring is calculated as:
PE = 1/2 kx2
Where k is the spring constant, and x is the displacement distance. As with lifted objects, the potential energy increases quadratically with displacement for a given spring. Stretching a spring 5cm from its rest position with a constant k = 100 N/m results in a potential energy of 0.5 x 100 N/m x (0.05m)2 = 0.125 J.
So in summary, potential energy can easily be observed and calculated when lifting objects against gravity or compressing/extending springs. The potential energy increases proportionally with height and displacement in these examples.
Comparing Potential and Kinetic Energy
Potential energy and kinetic energy are the two main forms of mechanical energy. While they seem quite different, they are intimately related. The key difference between them is that potential energy is stored energy, while kinetic energy is energy of motion.
Potential energy exists by virtue of an object’s position or configuration. For example, a ball held at a height above the ground has gravitational potential energy due to gravity’s influence on it. If released, this stored energy will be converted into kinetic energy as gravity accelerates the ball downward. The moving ball now has kinetic energy of motion.
Other forms of potential energy include elastic potential energy stored in stretched springs and chemical potential energy stored in batteries. In each case, the potential energy is converted to kinetic energy when released. A compressed spring will push outward, causing connected objects to move. Chemical reactions in a battery produce an electric current that powers kinetic motion.
According to the law of conservation of energy, the total mechanical energy in a closed system remains constant. Energy is never lost, but only converted between potential and kinetic forms. Understanding the relationship between potential and kinetic energy is key to analyzing mechanical systems across many fields of science and engineering.
Conservation of Energy
The law of conservation of energy states that the total energy in an isolated system remains constant. This means that energy cannot be created or destroyed, only converted from one form to another. In the context of potential and kinetic energy, this means that the total mechanical energy (potential energy + kinetic energy) stays the same.
When an object moves, it converts potential energy into kinetic energy. For example, when you hold a book above the ground, it has potential energy due to gravity. When you drop the book, this potential energy is converted into kinetic energy as the book gains speed. The total energy before and after dropping the book is the same.
The conservation of energy is an important concept in physics and engineering. It allows us to analyze mechanical systems like roller coasters, pendulums, and springs without having to account for energy losses or gains – we know that the total energy will remain the same. This makes calculations and analysis much simpler.
Applications of Potential Energy
Potential energy has many practical applications in fields like engineering, construction, and physics. Understanding potential energy is key to designing structures and devices that use gravity, motion, and energy storage effectively.
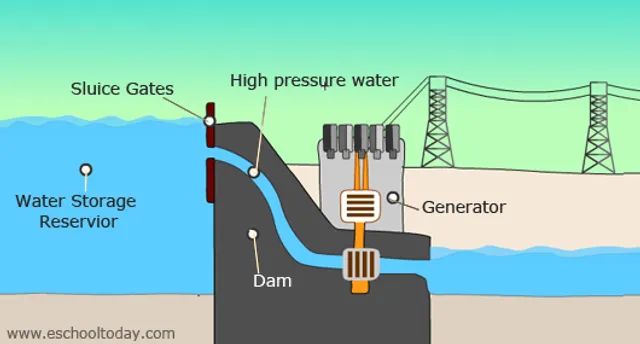
One of the most common applications is using the gravitational potential energy of water in hydroelectric dams. The dam stores water at a high elevation, giving it gravitational potential energy. When the water is released, it flows down through turbines, converting that potential energy into kinetic energy and electricity.
Another example is springs and elastic devices. The tension or compression of a spring gives it potential energy. When released, the spring converts the stored energy into kinetic energy. This allows springs to propel objects or absorb shocks and impacts.
Mass raised above the ground, like a rollercoaster going up a hill, also stores gravitational potential energy. Moving the mass downward converts this into kinetic energy, allowing the rollercoaster to accelerate and complete the ride.
Potential energy has many uses beyond these examples. Understanding how to calculate it from force allows engineers and physicists to quantify how much energy a system has available to do work. This knowledge enables innovative applications in renewable energy, construction, transportation, and more.
Practice Calculating Potential Energy
One of the best ways to get comfortable with calculating potential energy is to work through some practice problems. Let’s go through a few sample problems step-by-step:
Sample Problem 1
A 5kg book is lifted 2m above the ground. What is its potential energy?
Solution:
PE = mgh
m = 5kg
g = 9.8 m/s2
h = 2m
Plugging this into the equation:
PE = (5kg)(9.8 m/s2)(2m)
PE = 98 J
Sample Problem 2
A 12N force is used to lift a 4kg box 3m vertically. What is its potential energy?
Solution:
PE = Fh
F = 12N
h = 3m
Plugging this into the equation:
PE = (12N)(3m)
PE = 36J
Working through practice problems like these and checking your work is a great way to reinforce your understanding of calculating potential energy.